
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КУРСОВАЯ РАБОТА. Введение
| минобрнауки россии федеральное государственное бюджетное образовательное учреждение высшего образования «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» | |
| Институт (факультет) | Институт информациoнных технологий |
| Кафедра | Математики и информатики |
КУРСОВАЯ РАБОТА
| по дисциплине: Аспекты прикладной математики | |
| на тему | «Прикладные аспекты математики XIX века» |
|
| |
| Выполнила студентка группы 1ПДоб-15-31зп |
| группа |
| 44.03.05. Педагогическое образование. Математика. Информатика. |
| шифр, наименование |
| Зубова Светлана Васильевна |
| фамилия, имя, отчество |
| Руководитель: |
| Толстиков Алексей Валерианович |
| фамилия, имя, отчество |
| преподаватель |
| должность |
| Дата представления работы |
| «______»__________________2020г. |
| Заключение о допуске к защите |
| ________________________________________ Оценка _______________, _______________ |
| количество баллов |
| Подпись преподавателя_________________ |
Череповец, 2020 го
Оглавление
Введение
Раздел 1. Прикладные аспекты математики 19 века
Раздел 2. История становления прикладной составляющей
школьного математического образования
Заключение
Список использованной литературы
Введение
В истории математики существует несколько классификаций истории математики, по одной из них выделяются несколько этапов развития математических знаний:
Формирование понятия геометрической фигуры и числа как идеализации реальных объектов и множеств однородных объектов. Появление счёта и измерения, которые позволили сравнивать различные числа, длины, площади и объёмы.
Изобретение арифметических операций. Накопление эмпирическим путём (методом проб и ошибок) знаний о свойствах арифметических действий, о способах измерения площадей и объёмов простых фигур и тел. В этом направлении далеко продвинулись шумеро - вавилонские, китайские и индийские математики древности.
Появление в древней Греции дедуктивной математической системы, показавшей, как получать новые математические истины на основе уже имеющихся. Венцом достижений древнегреческой математики стали «Начала» Евклида, игравшие роль стандарта математической строгости в течение двух тысячелетий.
Математики стран ислама не только сохранили античные достижения, но и смогли осуществить их синтез с открытиями индийских математиков, которые в теории чисел продвинулись дальше греков.
В XVI-XVIII веках возрождается и уходит далеко вперёд европейская математика. Её концептуальной основой в этот период являлась уверенность в том, что математические модели являются своего рода идеальным скелетом Вселенной, и поэтому открытие математических истин является одновременно открытием новых свойств реального мира. Главным успехом на этом пути стала разработка математических моделей зависимости переменных величин (функция) и общая теория движения (анализ бесконечно малых). Все естественные науки были перестроены на базе новооткрытых математических моделей, и это привело к колоссальному их прогрессу.
В XIX-XX веках становится понятно, что взаимоотношение математики и реальности далеко не столь просто, как ранее казалось. Не существует общепризнанного ответа на своего рода «основной вопрос философии математики»: найти причину «непостижимой эффективности математики в естественных науках». В этом, и не только в этом, отношении математики разделились на множество дискутирующих школ. Наметилось несколько опасных тенденций: чрезмерно узкая специализация, изоляция от практических задач и др. В то же время мощь математики и её престиж, поддержанный эффективностью применения, высоки как никогда прежде.
Помимо большого исторического интереса, анализ эволюции математики представляет огромную важность для развития философии и методологии математики. Нередко знание истории способствует и прогрессу конкретных математических дисциплин; например, древняя китайская задача (теорема) об остатках сформировала целый раздел теории чисел.
Цель работы – исследовать прикладные аспекты математики 19 века.
Раздел 1. Прикладные аспекты математики 19 века
Неоспоримая эффективность применения математики в естествознании подталкивала учёных к мысли, что математика, так сказать, встроена в мироздание, является его идеальной основой. Другими словами, познание в математике есть часть познания реального мира. Многие учёные XVII-XVIII веков в этом и не сомневались. Но в XIX веке эволюционное развитие математики было нарушено, и этот, казавшийся непоколебимым, тезис был поставлен под сомнение.
В геометрии, алгебре, анализе появляются многочисленные нестандартные структуры с необычными свойствами: неевклидовы и многомерные геометрии, кватернионы, конечные поля, некоммутативные группы и т. п.
Объектами математического исследования всё больше становятся нечисловые объекты: события, предикаты, множества, абстрактные структуры, векторы, тензоры, матрицы, функции, многолинейные формы и т. д.
Возникает и получает широкое развитие математическая логика, в связи с чем появилось искушение связать именно с ней коренные основания математики.
Георг Кантор вводит в математику предельно абстрактную теорию множеств, а заодно понятие актуальной бесконечности произвольного масштаба. В конце века при попытке обосновать фундамент математики на основе теории множеств были обнаружены противоречия, которые заставили задуматься над непростыми вопросами: что означает «существование» и «истинность» в математике?
В целом в XIX веке роль и престиж математики в науке и экономике заметно растут, соответственно растёт и её государственная поддержка. Математика вновь становится по преимуществу университетской наукой.
Появляются первые математические сообщества: Лондонское, Американское, Французское, Московское, а также общества в Палермо и Эдинбурге.
Рассмотрим вкратце развитие основных областей математики в XIX веке.
1. Геометрия.
Если XVIII век был веком анализа, то XIX век по преимуществу стал веком геометрии. Быстро развиваются созданные в конце XVIII века начертательная геометрия (Монж, Ламберт) и возрождённая проективная геометрия (Монж, Понселе, Лазар Карно). Появляются новые разделы: векторное исчисление и векторный анализ, геометрия Лобачевского, многомерная риманова геометрия, теория групп преобразований. Происходит интенсивная алгебраизация геометрии – в неё проникают методы теории групп возникает алгебраическая геометрия. В конце века создана «качественная геометрия» – топология.
Дифференциальная геометрия получила мощный толчок после выхода чрезвычайно содержательного труда Гаусса «Общие исследования о кривых поверхностях» (1822), где впервые были явно определены метрика (первая квадратичная форма) и связанная с ней внутренняя геометрия поверхности. Исследования продолжила парижская школа. В 1847 году Френе и Серре опубликовали известные формулы Френе для дифференциальных атрибутов кривой.
Крупнейшим достижением стало введение понятия вектора и векторного поля. Первоначально векторы ввёл У. Гамильтон в связи со своими кватернионами (как их трёхмерную мнимую часть). У Гамильтона уже появилось скалярное и векторное произведение. Сверх того, Гамильтон ввёл дифференциальный («набла») и многие другие понятия векторного анализа, в том числе определение вектор функции и тензорного произведения.
Компактность и инвариантность векторной символики, использованной в первых трудах Максвелла, заинтересовали физиков; вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному исчислению современный вид.
Проективная геометрия после полутора веков забвения вновь привлекла внимание – сначала Монжа, затем его учеников – Понселе и Лазара Карно. Карно сформулировал «принцип непрерывности», который позволяет сразу распространить некоторые свойства исходной фигуры на фигуры, полученные из неё непрерывным преобразованием (1801-1806). Несколько позднее Понселе ясно определил проективную геометрию как науку о проективных свойствах фигур и дал систематическое изложение её содержания (1815). У Понселе уже полностью легализованы бесконечно удалённые точки (даже мнимые). Он сформулировал принцип двойственности (прямых и точек на плоскости).
С конца 1820-х годов формируется школа проективных геометров в Германии (Мёбиус, Плюккер, Гессе, Штейнер и другие). В Англии ряд работ опубликовал Кэли. При этом стали использоваться и аналитические методы, особенно после открытия Мёбиусом однородных проективных координат, включающих и бесконечно удалённую точку. Во Франции работы Понселе продолжил Мишель Шаль.
Большое влияние на развитие математики имела знаменитая речь Римана (1854) «О гипотезах, лежащих в основании геометрии». Риман определил общее понятие n-мерного многообразия и его метрику в виде произвольной положительно определённой квадратичной формы. Далее Риман обобщил теорию поверхностей Гаусса на многомерный случай; при этом появляются знаменитый риманов тензор кривизны и другие понятия римановой геометрии. Существование неевклидовой метрики, по Риману, может объясняться либо дискретностью пространства, либо некими физическими силами связи. В конце века Г. Риччи завершает классический тензорный анализ.
Во второй половине XIX века наконец привлекает общее внимание геометрия Лобачевского. Тот факт, что даже у классической геометрии существует альтернатива, произвёл огромное впечатление на весь научный мир. Он также стимулировал переоценку многих устоявшихся стереотипов в математике и физике.
Ещё один переломный момент развития геометрии наступил в 1872 году, когда Феликс Клейн выступил со своей «Эрлангенской программой». Он классифицировал геометрические науки по используемой группе преобразований – вращения, аффинные, проективные, общие непрерывные и т. п. Каждый раздел геометрии изучает инварианты соответствующей группы преобразований. Клейн рассмотрел также важнейшее понятие изоморфизма (структурного тождества), который называл «перенесением». Тем самым был намечен новый этап алгебраизации геометрии, второй после Декарта.
В 1872-1875 годах Камилл Жордан опубликовал ряд работ по аналитической геометрии n-мерного пространства (кривых и поверхностей), а в конце века он предложил общую теорию меры.
В самом конце века рождается топология, сначала под названием analysis situs. Топологические методы фактически в ряде работ использовали Эйлер, Гаусс, Риман, Жордан и др. Вполне ясно предмет новой науки описывает Феликс Клейн в своей «Эрлангенской программе». Окончательно комбинаторная топология оформилась в работах Пуанкаре (1895-1902).
2. Математический анализ.
Анализ в XIX веке развивался путём быстрой, но мирной эволюции.
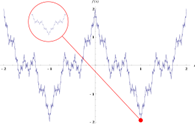
Пример Вейерштрасса: всюду непрерывная, но нигде не дифференцируемая функция
Наиболее существенной переменой стало создание фундамента анализа (Коши, затем Вейерштрасс). Благодаря Коши мистическое понятие актуального бесконечно малого исчезло из математики (хотя в физике оно используется до сих пор). Были поставлены вне науки и сомнительные действия с расходящимися рядами. Коши построил фундамент анализа на основе теории пределов, близкой к ньютоновскому пониманию, и его подход стал общепринятым; анализ стал менее алгебраичным, но более надёжным. Тем не менее до уточнений Вейерштрасса многие предрассудки ещё сохранялись: например, Коши верил, что непрерывная функция всегда дифференцируема, а сумма ряда из непрерывных функций непрерывна.
Широчайшее развитие получила теория аналитических функций комплексного переменного, над которой работали Лаплас, Коши, Абель, Лиувилль, Якоби, Вейерштрасс и другие. Значительно расширился сам класс специальных функций, особенно комплексных. Главные усилия были направлены на теорию абелевых функций, которые не вполне оправдали возлагавшиеся на них надежды, но тем не менее способствовали обогащению аналитического инструментария и созданию в XX веке более общих теорий.
Многочисленные прикладные задачи деятельно стимулировали теорию дифференциальных уравнений, выросшую в обширную и плодотворную математическую дисциплину. Детально исследованы основные уравнения математической физики, доказаны теоремы существования решения, создана качественная теория дифференциальных уравнений (Пуанкаре).
К концу века происходит некоторая геометризация анализа – появляются векторный анализ, тензорный анализ, исследуется бесконечно мерное функциональное пространство. Компактная инвариантная запись дифференциальных уравнений гораздо удобнее и нагляднее, чем громоздкая координатная запись.
3. Алгебра и теория чисел.
Намеченные у Эйлера аналитические методы помогли решить немало трудных проблем теории чисел (Гаусс, Дирихле и другие). Гаусс дал первое безупречное доказательство основной теоремы алгебры. Жозеф Лиувилль доказал существование бесконечного количества трансцендентных чисел (1844, подробнее в 1851), дал достаточный признак трансцендентности и построил примеры таких чисел в виде суммы ряда. В 1873 году Шарль Эрмит публикует доказательство трансцендентности числа Эйлера, а в 1882 году Линдеман применил аналогичный метод и к числу.
У. Гамильтон открыл удивительный некоммутативный мир кватернионов.
4. Возникла геометрическая теория чисел (Минковский).
Эварист Галуа, опередивший своё время, представляет глубокий анализ решения уравнений произвольных степеней. Ключевыми понятиями исследования оказываются алгебраические свойства связанных с уравнением группы подстановок и полей расширения. Галуа завершил работы Абеля, доказавшего, что уравнения степени выше 4-й неразрешимы в радикалах.
По мере усвоения идей Галуа, со второй половины века, быстро развивается общая алгебра. Жозеф Лиувилль публикует и комментирует работы Галуа. В 1850-е годы Кэли вводит понятие абстрактной группы. Термин «группа» становится общепринятым и проникает практически во все области математики, а в XX веке – в физику и кристаллографию.
Формируется понятие линейного пространства (Грассман и Кэли, 1843-1844). В 1858 году Кэли публикует общую теорию матриц, определяет операции над ними, вводит понятие характеристического многочлена. К 1870 году доказаны все базовые теоремы линейной алгебры, включая приведение к жордановой нормальной форме.
В 1871 году Дедекинд вводит понятия кольца, модуля и идеала. Он и Кронекер создают общую теорию делимости.
В конце XIX века в математику входят группы Ли.
5.Теория вероятностей.
На первое место выходят теория ошибок, статистика и физические приложения. Этим занимались Гаусс, Пуассон, Коши. Была выявлена важность нормального распределения как предельного во многих реальных ситуациях.
Во всех развитых странах возникают статистические департаменты/общества. Благодаря работам Карла Пирсона возникает математическая статистика с проверкой гипотез и оценкой параметров.
Всё же математические основы теории вероятностей в XIX веке ещё не были созданы, и Гильберт в начале XX века отнёс эту дисциплину к прикладной физике.
6. Математическая логика.
После неудачи проекта «Универсальной характеристики» Лейбница прошло полтора века, прежде чем попытка создать алгебру логики повторилась. Но повторилась она на новой основе: концепция множества истинности позволила построить математическую логику как теорию классов, с теоретико-множественными операциями. Пионерами стали британские математики Август (Огастес) де Морган и Джордж Буль.
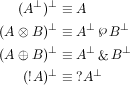
7. Законы де Моргана в символике их автора.
В работе «Формальная логика» (1847) де Морган описал понятие универсума и символы для логических операторов, записал известные «законы де Моргана». Позже он ввёл общее понятие математического отношения и операций над отношениями.
Джордж Буль независимо разработал свой, более удачный, вариант теории. В своих работах 1847-1854 годов он заложил основы современной математической логики и описал алгебру логики (булеву алгебру). Появились первые логические уравнения, введено понятие конституэнты (разложения логической формулы).
Уильям Стенли Джевонс продолжил систему Буля и даже построил «логическую машину», способную решать логические задачи. В 1877 году Эрнест Шрёдер сформулировал логический принцип двойственности. Далее Готлоб Фреге построил исчисление высказываний. Чарльз Пирс в конце XIX века изложил общую теорию отношений и пропозициональных функций, а также ввёл кванторы. Современный вариант символики предложил Пеано. После этого всё было готово для разработки в школе Гильберта теории доказательств.
8. Обоснование математики.
К началу XIX века относительно строгое логическое (дедуктивное) обоснование имела только евклидова геометрия, хотя строгость её уже тогда справедливо считалась недостаточной. Свойства новых объектов (например, комплексных чисел, бесконечно малых и т. д.) попросту считались в целом такими же, как у объектов уже известных; если же такая экстраполяция была невозможна, свойства подбирались опытным путём.
Построение фундамента математики началось с анализа. В 1821 году Коши опубликовал «Алгебраический анализ», где чётко определил основные понятия на основе концепции предела. Всё же он сделал ряд ошибок, например, почленно интегрировал и дифференцировал ряды, не доказывая допустимость таких операций. Завершил фундамент анализа Вейерштрасс, который выяснил роль важного понятия равномерной непрерывности. Одновременно Вейерштрасс (1860-е годы) и Дедекинд (1870-е) дали обоснование теории вещественных чисел.
1837 год: Уильям Гамильтон строит модель комплексных чисел как пар вещественных.
В 1870-е годы были легализованы неевклидовы геометрии. Их модели на базе евклидового пространства доказали, что они так же непротиворечивы, как и геометрия Евклида.
1879 год: Фреге публикует систему аксиом математической логики.
1888 год: Дедекинд предлагает набросок системы аксиом для натуральных чисел. Годом позже законченную систему аксиом предложил Пеано.
1899 год: выходят в свет «Основания геометрии» Гильберта.
В итоге к концу века почти вся математика была построена на базе строгой аксиоматики. Непротиворечивость основных разделов математики (кроме арифметики) была строго доказана (точнее говоря, сведена к непротиворечивости арифметики). Аксиоматический фундамент для теории вероятностей и теории множеств появился позже, в XX веке.
9. Теория множеств и антиномии.
В 1873 году Георг Кантор ввёл понятие произвольного числового множества, а затем и общее понятие множества – самого абстрактного понятия в математике. С помощью взаимно-однозначных отображений он ввёл понятие равномощности множеств, потом определил сравнение мощностей на больше - меньше и, наконец, классифицировал множества по величине их мощности: конечные, счётные, континуальные и т. д.
Иерархию мощностей Кантор рассматривал как продолжение иерархии (порядка) целых чисел (трансфинитные числа). Тем самым в математику была введена актуальная бесконечность – понятие, которого прежние математики старательно избегали.
На первых порах теория множеств встретила у многих математиков доброжелательный приём. Она помогла обобщить жордановскую теорию меры, успешно использовалась в теории интеграла Лебега и многими рассматривалась как основа будущей аксиоматики всей математики. Однако последующие события показали, что привычная логика не годится при исследовании бесконечности, а интуиция не всегда помогает сделать правильный выбор.
Первое противоречие обнаружилось при рассмотрении самого большого множества – множества всех множеств (1895). Его пришлось исключить из математики как недопустимое. Однако появились и другие противоречия (антиномии).
Анри Пуанкаре, который вначале принял теорию множеств и даже использовал в своих исследованиях, позже решительно отверг её и назвал «тяжёлой болезнью математики». Однако другая группа математиков, включая Бертрана Рассела, Гильберта и Адамара, выступили в защиту «канторизма».
Положение усугубило открытие «аксиомы выбора» (1904, Цермело), которая, оказывается, неосознанно применялась во многих математических доказательствах (например, в теории вещественных чисел). Эта аксиома объявляет существующим множество, о составе которого ничего не известно, и это обстоятельство ряд математиков посчитал совершенно неприемлемым, тем более что некоторые следствия аксиомы выбора противоречили интуиции (парадокс Банаха – Тарского и др.).
В начале XX века удалось согласовать вариант теории множеств, свободный от обнаруженных ранее противоречий (теория классов), так что большинство математиков приняли теорию множеств. Однако былого единства математики больше нет, часть научных школ стали развивать альтернативные взгляды на обоснование математики.
Раздел 2. История становления прикладной составляющей школьного математического образования
Цифирная школа, школа математических и навигацких наук (1701), арифметика Л. Магницкого (1703), утилитарный характер изучения математики, народные училища (1786), трехуровневая система образования (первая половина XIX), реальные училища (1872), профессиональная ориентация обучения математике.
Анализ исторических документов, учебников математики разных лет, исследований по истории образования показал, что в истории отечественного математического образования всегда присутствовала тема связи обучения с жизнью. Приложения математики в результате реформирования, трансформации образовательных целей то выступали на первый план, то выполняли вспомогательную роль в обучении.
Как свидетельствуют Ю.М. Колягин, Т.С. Полякова, В.В. Орлов в ХVI–XVII веках системы образования в современном понимании не существовало. Математика изучалась ограниченным кругом людей для осуществления практической деятельности, связанной с ведением хозяйства, торговли, межеванием земель, податными сборами и т.п. Обучение математике носило рецептурный характер, математическая теория излагалась в связи с решением какой-либо задачи, сюжет которой был связан с событиями, возникающими в реальной жизни.
Массовая образовательная система в России (цифирные школы) появилась только в эпоху Петра I. В так называемых «Цифирных книгах» учебный материал был представлен в виде задач-примеров из жизненной практики, связанных с выплатой жалования, вычислением земельных площадей, совершением торговых сделок. Математические дисциплины (арифметика, геометрия, тригонометрия) в этот период, как отмечает А.Я. Халамайзер, выделились в отдельные предметы. Содержание образования по-прежнему было нацелено на подготовку обучающихся к определенной профессиональной деятельности, т.е. носило контекстный характер. В качестве примера автор приводит факт открытия в 1701 г. «Школы математических и навигацких наук». Математика была разделена не только на отдельные дисциплины, но и на теоретическую (чистую) и практическую (прикладную), показывающую пути использования математических знаний в профессиональной деятельности.
В этой школе, помимо учителей-иностранцев, преподавал Леонтий Магницкий – один из наиболее образованных людей своего времени. Широко известная «Арифметика» Л. Магницкого, изданная в 1703 году, содержала не только основы математических знаний, но и сведения по мореходной астрономии и навигации с необходимыми таблицами и задачами, что, несомненно, подчеркивало не просто прикладной, а утилитарный характер изучения математики в этот период. И.К. Андронов отмечает, что все эти прогрессивные изменения были обусловлены развитием самой математики как науки.
На XVII–XVIII вв. приходится период, который А.Н. Колмогоров условно называет периодом «высшей математики». Дальнейшее развитие науки на этом временном отрезке было обусловлено возникновением практических потребностей в технике, военном деле, навигации и картографии. В конце XVIII начале XIX века, как пишут Ю.М. Колягин, Т.С. Полякова, российское математическое образование неоднократно подвергалось реформированию. Основным объектом реформ являлось содержание образования. Проанализируем изменения, происходившие в прикладной составляющей содержания математического образования в XVIII–XIX вв.
Позднее, в конце 20-х – начале 30-х гг. XIX века математика как учебная дисциплина существенно трансформировалась: совершенно упразднялась прикладная математика, изучение теоретического материала значительно ограничивалось. В.В. Орлов акцентирует внимание на следующем факте: в средних учебных заведениях давались только те математические знания, которые были необходимы в определенных профессиях, в промышленности, армии и флоте. Эти знания не были организованы в цельную систему, отсутствовали научная строгость, логически выдержанная последовательность в изложении материала.
Через небольшой период времени стало понятно, что математическое образование в таком усеченном виде существовать дальше не может. В первой половине ХIХ века в результате образовательных реформ в России была создана, как отмечает Т.С. Полякова, трехуровневая система математического образования, включавшая начальное (приходские и уездные училища), среднее (гимназии) и высшее математическое образование (университеты).
Математика в гимназиях, как это было и ранее, делилась на «чистую» и «прикладную». Однако число практических приложений в учебных пособиях для гимназий постепенно уменьшается. Их основной функцией становится иллюстрация изучаемой теории, а не профессиональная подготовка. Содержательно прикладные геометрические задачи по-прежнему сводятся к измерениям и построениям на местности.
Подтверждение этому находим в учебнике по геометрии для гимназий Ф. Буссе (1845 г.). Прикладные задачи собраны в небольшой (всего 7 задач) раздел «Некоторые задачи из практической геометрии». В предисловии к этому разделу автор поясняет: «Практическая геометрия заключает в себе правила, по которым, с помощью известных орудий, можно означать на поверхности земли линии, углы, фигуры и измерять их; определять высоты предметов и расстояния между ними. Здесь будут показаны самые простейшие задачи, как применения некоторых теорем планиметрии». Вот примеры задач из этого раздела:
üВ данной точке D данной прямой DN на земле отложить угол, равный данному углу ВАС.
üИзмерить высоту приступного предмета.
üИзмерить высоту неприступного предмета.
Действительно, задачи (вместе с решениями) напоминают некоторые правила, применимые к целому ряду реальных ситуаций. Это связано с традициями обучения, принятыми в конце ХIХ века: способы решения задач и примеров часто заучивались как теория, поэтому задачи и формулировались «в общем виде».
В другом учебном издании того же временного периода, «Практические упражнения в геометрии…» (1844 г.), также имеется отдельный раздел – «Задачи, относящиеся к практической геометрии». Однако собранные в нем задачи уже не представляют собой правила для заучивания, а предназначены для проверки знаний и повторения изученного. Один из его авторов, известный педагог-математик П.С. Гурьев, придавал очень большое значение задачам в обучении математике. По его мнению, главная роль задач состоит в развитии мышления, кроме того, они должны вызывать у учеников интерес. Такой взгляд на обучение
математике, по мнению В.Е. Прудникова, был совершенно новым для своего времени. Многие задачи из рассматриваемого пособия хорошо известны нам и сегодня. Приведем наиболее узнаваемые примеры:
üОпределить ширину реки, не переезжая через нее.
üКак найти высоту какого-либо предмета, например, дерева, посредством отбрасываемой им тени.
üКак измерить высоту горы, которой вершина доступна.
В программе по математике, составленной в 1852 году, которую анализирует Ю.М. Колягин, по-прежнему сохраняется особое внимание к решению задач практического содержания и рассмотрению приложений теории к практике14. Предусматривалось даже проведение измерительных работ на местности с использованием различных приборов. Ранее, как видно из примеров, этот материал также присутствовал, но в виде отдельных задач. С этими приложениями математики мы неоднократно встретимся и в дальнейшем при анализе учебной математической литературы для школьников различных временных периодов.
Примерно в это же время, как указывает Л.Б. Модзалевский, осознавая необходимость изменений в практике обучения, Н.И. Лобачевский участвует в создании учебных программ для училищ и гимназий. В «Наставлениях учителям математики в гимназиях» он подчеркивает, что цель и сущность математического образования состоит «в двоякой пользе сего учения: … применение его к потребностям в нашей жизни и дальнейшее развитие самой науки».
В конце ХIХ в., как указывает В.В. Орлов, происходит расширение сети образовательных учреждений. Вначале по уставу 1864 г гимназии были разделены на классические и реальные. В реальных гимназиях большее внимание уделялось преподаванию математики, физики, естествознанию и космографии, а в гимназиях превалировал гуманитарный характер
обучения. Впоследствии реальные гимназии будут преобразованы в реальные училища, обучение в которых станет профессионально ориентированным. Отметим интересный факт. Права выпускников реальных училищ были урезаны. В отличие от гимназистов, они не могли поступать в университеты, где значимое место отводилось занятию теорией наук.
В 1872 году в России, как пишет А.В. Ланков, был принят и утвержден устав реальных училищ. В них должны были давать «общее образование, приспособленное к практическим потребностям и к приобретению технических познаний». Поэтому в учебных пособиях для реальных училищ приложения математики заняли не последнее место.
Подтвердим этот вывод на примере двух таких пособий – М.Ф. Борышкевича и С.В. Маракуева. Авторы единодушно считают необходимым познакомить ученика с приложениями математики, по словам С.В. Маракуева, «не только с отвлеченными истинами, но и с наиболее употребительными их применениями в жизни…». Задачи, связанные с приложениями математики, включены в большинство изучаемых разделов в обоих пособиях. Эти задачи используются не только для повторения, как у П.С. Гурьева, но и при изучении теоретических вопросов. Так, например, при изложении свойств перпендикуляра и наклонных линий, учащимся предварительно предлагается решить следующую задачу:
üИзмерить расстояние от сучка в доске стола до его края. Сюжеты прикладных задач затрагивают как традиционные темы для учебников того времени (построения и измерения на местности, устройства измерительных приборов), так и вопросы торговли, строительства, столярного дела. Интересно отметить, что не все сюжеты носят утилитарный характер. Отдельные задачи призваны познакомить учащихся с устройством окружающего мира, возможно не доступного для непосредственного ведения хозяйственной и производственной деятельности. В подтверждение этому приведем задачу из пособия М. Борышкевича:
üОпределить окружность Луны, когда известно, что диаметр ее равен 468 географических миль.
Для нашего анализа также представляет интерес пособие Г.Я. Юревича «Краткая геометрия для двуклассных сельских училищ» (1912). Это пособие предназначено для изучения начального курса геометрии. Существовало два типа такого курса: элементарный и элементарно теоретический. Двуклассные училища открывались в сельской местности, поэтому обучение в них велось по элементарному курсу, носившему практический характер, что соответствовало потребностям крестьянского труда. Первая часть книги охватывала «приготовительный» курс и являлась универсальной по содержанию для учебного заведения любого профиля.
А во вторую часть, содержащую сокращенный курс элементарной геометрии, были включены сведения о практических применениях геометрии к съемке планов, измерению поверхностей и вычислению объемов тел. Имелись прикладные задачи, непосредственно связанные с сельскохозяйственным трудом. Например:
üСколько пудов прессованного сена может поместиться в сарае, длина которого равна 12 саженям, ширина 4 саж. и вышина 2 саж., если кубическая сажень прессованного сена весит 400 пудов?
Итак, изучение прикладных аспектов математической науки являлось неотъемлемой частью математического образования в России на рубеже XVIII–XIX веков. Изучение приложений теории к практике имело большое значение как для подготовки к профессиональной деятельности, так и для воспитания образованного человека. Математическое образование в целом на этом историческом этапе начинает приобретать черты общекультурной значимости. Этот период будем считать периодом становления не только математического образования, но и его прикладной составляющей.
Приложения математики на начальном этапе (ХVII в.) предстают в виде рецептов разрешения конкретных ситуаций. Для ХVIII века основным было практическое направление, реализуемое в сфере профессионального образования. В конце ХVIII века теоретическое и практическое направления в обучении стали сближаться. Однако до ХIХ века изучалась именно прикладная геометрия, а ее теоретическая составляющая служила лишь инструментом решения задач из практики. В учебной литературе XVIII–ХIХ вв. содержатся прикладные задачи, практические задания, а также отдельные сведения о применении математики к наиболее распространенным и востребованным на тот период времени видам деятельности человека.
Для геометрии часто встречающимися примерами приложений были: использование геометрических построений для съемки планов местности, вычисление площадей поверхностей и объемов тел в сельскохозяйственной деятельности, использование свойств фигур в столярном и строительном деле.
Приоритетной целью использования приложений математики в обучении на протяжении рассмотренного времени (ХVII–ХIХ вв.) являлась профессиональная ориентация обучения. Далее по убыванию значимости – получение полезных для дальнейшей жизни сведений дополнительно к изучаемому математическому материалу; ознакомление с устройством окружающего мира; поддержание интереса к предмету.
Мощным толчком к развитию российской науки послужили реформы М. М. Сперанского. В начале XIX века было создано Министерство народного просвещения, возникли учебные округа, и гимназии стали открываться во всех крупных городах России. При этом содержание курса математики было довольно обширным – алгебра, тригонометрия, приложения к физике и др.
Начали открываться новые университеты – в Казани и Харькове (1804), в Петербурге (1819), в Киеве (1834). Все они в обязательном порядке имели физико-математический факультет. В XIX веке молодая российская математика уже выдвинула учёных мирового уровня. Михаил Васильевич Остроградский разрабатывал преимущественно прикладной математический анализ. В его работах исследуется распространение тепла, волновое уравнение, теория упругости, электромагнетизм. Занимался также теорией чисел.
Академик пяти мировых академий. Николай Иванович Лобачевский прославился своей самоотверженной борьбой против догмата евклидовости пространства. Он построил
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|