Компланарные вектора. Равные вектора. Единичный вектор

Компланарные вектора

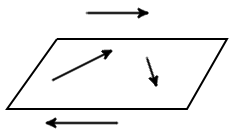
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Равные вектора

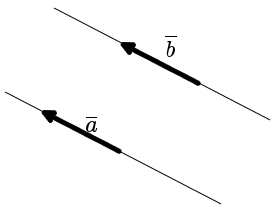
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b, если a↑↑b и |a| = |b|.

Единичный вектор

Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.