Двугранный угол — это часть пространства, заключённая между двумя полуплоскостями, имеющими одну общую границу.

Тема. Двугранный угол. Перпендикулярность плоскостей

Теоретический материал

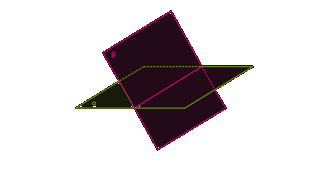
Если в пространстве пересекаются две плоскости, получаются четыре двугранных угла (аналогично как при пересечении двух прямых получаются четыре угла). Рассмотрим один из них.

Полуплоскости α и β, образующие двугранный угол, называются его гранями.

Общая прямая a этих граней называется ребром двугранного угла.

Выберем на ребре a двугранного угла произвольную точку C и проведём две пересекающиеся прямые AC⊥a и BC⊥a, а через эти прямые — плоскость γ перпендикулярно ребру a.

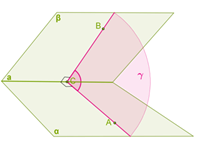
Линии пересечения AC и BC полуплоскостей α и β с плоскостью γ образуют некоторый угол ∡ACB. Этот угол называется линейным углом двугранного угла. Величина линейного угла не зависит от выбора точки C на ребре a.

Обрати внимание!

Величина двугранного угла 0°< ∡ACB <180°.

Если плоскости параллельны, то угол между ними равен 0° по определению.

Определение. Если при пересечении плоскостей один из двугранных углов составляет 90°, то три остальных угла — тоже 90°. Эти плоскости называют перпендикулярными.

Следующие теоремы, которые здесь приведём без доказательств, могут пригодиться при решении задач.

Теорема 1. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Теорема 2. Плоскость, перпендикулярная прямой, по которой пересекаются две плоскости, перпендикулярна каждой из этих плоскостей.

Теорема 3. Если две плоскости перпендикулярны, и в одной из них прямая проведена перпендикулярно линии пересечения плоскостей, то эта прямая перпендикулярна второй плоскости.

12 Следующая ⇒