Глава III. Расширение понятий о числе.

Глава III. Расширение понятий о числе.

Положительные рациональные числа.

§ 1. Понятие дроби и положительного рационального числа.

Множество положительных рациональных чисел, его свойства.

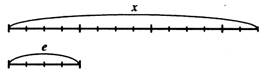
Пусть требуется измерить длину отрезка хс помощью единичного отрезка е. При измерении оказалось, что отрезок х состоит из трех отрезков, равных е, и отрезка, который короче отрезка е. В этом случае длина отрезка х не может быть выражена натуральным числом.

Однако, если отрезок еразбить на 4 равные части, то отрезок хокажется состоящим из 14 отрезков, равных четвертой части отрезка е. И тогда, говоря о длине отрезка х, мы должны указать два числа 4 и 14: четвертая часть отрезка еукладывается в отрезке точно 14 раз.

Поэтому условились длину отрезка хзаписывать в виде 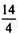е, где символ 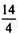называется дробью.

Опр. 1. Пусть даны отрезок a и единичный отрезок е. Если отрезок a состоит из m отрезков, равных n-ой части отрезка е, то длина отрезка a

может быть представлена в виде n Этот символ называется дробью.

В записи дроби числа ти п - натуральные, тназывается числителем, п - знаменателем дроби.

Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.

Опр. 2.Дроби, выражающие длину одного и того же отрезка при единице длиные,называют равными дробями.

m p

Теорема 1. Для того, чтобы дроби n и q были равны, необходимо и достаточно, чтобы mq = np.

12 Следующая ⇒