
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Неопределенный интеграл.. Интегрирование рациональных, иррациональных, тригонометрических функций
10. Неопределенный интеграл.
Интегрирование рациональных, иррациональных, тригонометрических функций
Справочный материал
I Интегрирование рациональных дробей вида 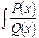 dx, где P(x), Q(x) - многочлены
dx, где P(x), Q(x) - многочлены
1. Простейшие дроби
1) 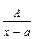
2) 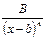
3) 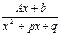
4) 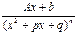 , где
, где 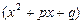 не имеет действительных корней.
не имеет действительных корней.
2. Интегрирование рациональных дробей
Дробь 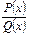 - правильная, если степень P(x) меньше степени Q(x). В противном случае дробь – неправильная.
- правильная, если степень P(x) меньше степени Q(x). В противном случае дробь – неправильная.
При интегрировании неправильной дроби, необходимо выполнить деление с остатком и представить данную дробь в виде суммы некоторого многочлена и правильной дроби: 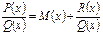
3. Разложение правильной рациональной дроби 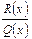 на сумму простейших
на сумму простейших
1) Разложить знаменатель Q(x) на линейные и квадратичные множители, не имеющие действительных корней: 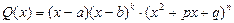
2) Представить дробь 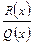 в виде суммы простейших дробей, соответствующих множителям знаменателя
в виде суммы простейших дробей, соответствующих множителям знаменателя
| Множитель Q | Слагаемые разложения | |
| 1. | х - a | 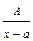
|
| 2. | (x - b)k | 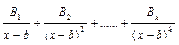
|
| x2 + px + q | 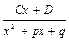
| |
| 4. | (x2 + px + q)n | 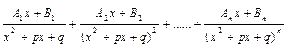
|
Аi ,Bi , C, D - некоторые константы, для нахождения которых используют:
а) метод неопределенных коэффициентов – приравнивание коэффициентов при одинаковых степенях х;
б) метод частных значений – подстановка вместо х стольких произвольных значений (начиная с корней знаменателя), сколько имеется неопределенных коэффициентов.
в) комбинированный метод.
В результате получают СЛУ относительно искомых коэффициентов.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|