Задания. Структура отчета. Пример выполнения задания

4. Задания

1. Изучить методические указания к выполнению практической работы.

2. Выполнить индивидуальное задание.

3. Оформить отчет по практической работе.

5. Структура отчета

1. Номер и наименование практической работы.

2. Цель работы.

3. Задание.

4. Выполнение работы.

6. Пример выполнения задания

Задача 1. Решите простейшие тригонометрическое уравнение: .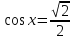

Решение: Согласно формуле (1) находим: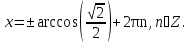

Задача 2. Решите простейшие тригонометрическое уравнение:

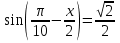
Решение: Функция синус нечетна. Поэтому 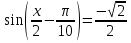. По формуле (2)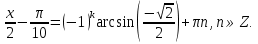

Так как 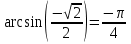, имеем: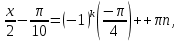

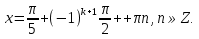
Задача 3. Решите уравнение: 2 sin x+ 3 cos x = 0.

Решение:

2 sin x+ 3 cos x = 0 | : cos x ≠ 0

2 tg x + 3 =0

tg x = -1,5

х= arctg (-1,5) + πk, k Z или х = - arctg 1,5 + πk, k Z

Ответ: - arctg 1,5 + πk, k Z.

Задача 4. Решите уравнение: 2 sin² х - 3 sinх cos х - 5 cos²х =0

Решение: 2 sin² х - 3 sinх cos х - 5 cos²х =0

2 sin² х - 3 sinх cos х - 5 cos²х =0 | : cos²х ≠ 0

2 tg ²x - 3 tg x - 5 = 0

замена tg x = t

2 t² – 3 t – 5 =0

t₁= -1; t₂= 2,5

Решением уравнения tg х = -1 являются числа вида х = -π/2 + πk , k Z.

Решением уравнение tg х = 2,5 являются числа вида х = arctg 2,5+ πn, n Z.

Ответ: -π/2 + πk , arctg 2,5+ πn, n, k Z.

Задача 5. Решить уравнение 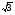sin x + cos x = 1

Решение: 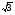sin x + cos x = 1

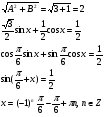
Ответ: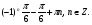

Задача 6. Решите уравнение: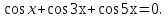

Решение: Группируя первый и последний члены и применяя формулу суммы косинусов, получим

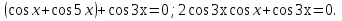
Следовательно, 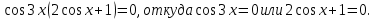Решая уравнение 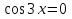, находим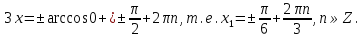

Задача 7. Решите уравнение: sin² х + 5 sin х - 6 =0.

Решение: Введем замену sin х = z, 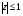, решая квадратное уравнение

z² + 5 z - 6 = 0, находим z₁= 1; z₂= -6 (не удовлетворяет условию )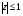

Решением уравнения sin х = 1 являются числа вида х = π/2 +2 π k, k Z.

Ответ: π/2 +2 π k, k Z.