Задание 3.1. Рекурсивные функции

Задание 3.1. Рекурсивные функции

Найдите n-ый член геометрической прогрессии, заданной первым членом и разностью.

Задание 3.2. Разработка рекурсивной триады

Для любых положительных чисел n и m найдите коэффициенты Безу, то есть такие целые a и b, что выполняется равенство: nod (n, m) = an + bm (где nod (n, m) – наибольший общий делитель n и m).

Задание 3.3. Рекурсивные методы в решении задач

Задача о коне Аттилы («Трава не растет там, где ступил мой конь!»). На шахматной доске стоят белый конь и черный король. Некоторые поля доски считаются «горящими». Конь должен дойти до неприятельского короля, повергнуть его и вернуться на исходное место. При этом ему запрещено становиться как на горящие поля, так и на поля, которые уже пройдены.

Задание 1.1. Линейные программы

Пуля, летящая со скоростью 400 м/с, ударяется в земной вал и проникает в него на глубину 36 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 18 см? На какой глубине скорость пули уменьшилась в 3 раза? Движение считать равноускоренным.

Текст программы:

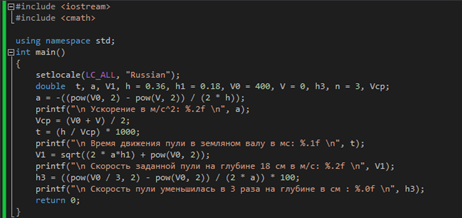
Контрольный пример:

Задание 1.2. Составление логических выражений

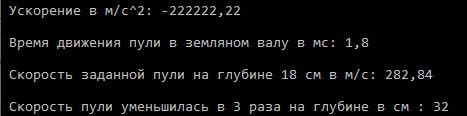
Сумма двух первых цифр заданного четырехзначного числа N равна произведению двух последних.

Текст программы:

Контрольный пример:

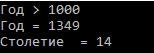
Задание 1.3. Условный оператор

По четырехзначному номеру года, запрошенному с клавиатуры определите номер столетия (например, для 1492 г. – ответ XV век, для 1812 г. – XIX век). Учесть, что началом века считается первый, а не нулевой, год. (То есть, 2000-й год – последний год XX века).

Текст программы:

Контрольный пример:

Задание 1.4. Оператор выбора (варианта)

В некотором учебном заведении действуют следующие правила приема. Абитуриенты сдают три экзамена. Если они набирают не менее 13 баллов, то это дает право поступить на дневное отделение, от 10 до 12 – на вечернее, от 8 до 9 – на заочное; ниже 8 баллов означает отказ в приеме на учебу. Написать программу, которая в зависимости от суммы набранных баллов сообщает абитуриенту его права на поступление.

Текст программы:

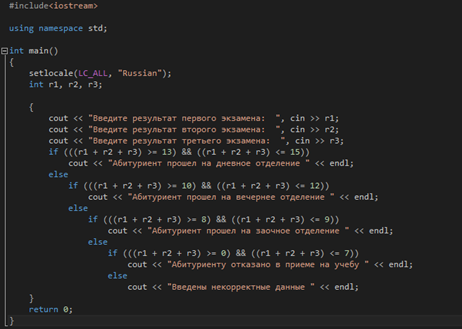
Контрольный пример:

Задание 1.5. Цикл с параметрами

Составить программу, которая находит наибольшее значение отношения n-значного числа к сумме его цифр (1 £ n £ 59).

Текст программы:

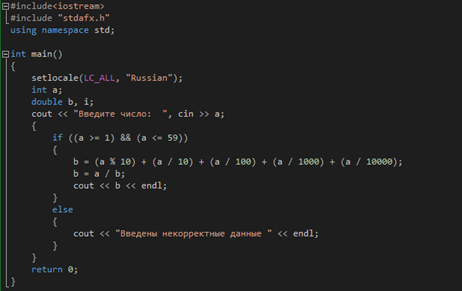
Контрольный пример:

Задание 1.6. Цикл с предусловием и постусловием

В водоеме 100 т рыбы. Каждый год рыболовецкая бригада вылавливает 15т. Воспроизводство рыбы 5% в год. Для сохранения воспроизводства необходимо прекращать лов, когда в водоеме ее остается менее 5 т. Через сколько лет лов рыбы должен быть прекращен?

Текст программы:

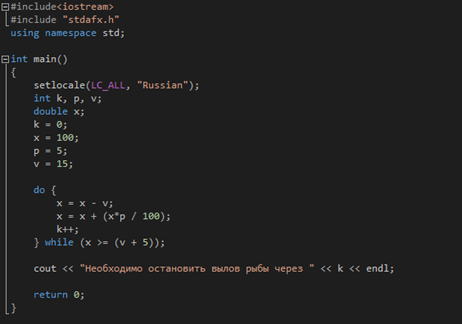
Контрольный пример:

⇐ Предыдущая 1 234 Следующая ⇒