
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Перпендикулярность плоскостей
Перпендикулярность плоскостей
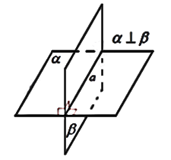
| Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен 90∘ . |
Признак перпендикулярности двух плоскостей
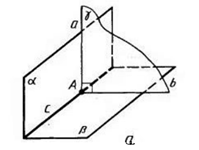
Теорема.Пусть нам даны плоскости α и β, которые пересекаются по прямой AC. Пусть прямая AB, лежащая в плоскости α перпендикулярна плоскости β
| Доказательство:Так как прямая AB перпендикулярна плоскости β, то она перпендикулярна и прямой AC. Проведем дополнительно прямую AD в плоскости β, перпендикулярно прямой AC. Получаем, что угол BAD - линейный угол двугранного угла, равный 90∘. То есть, по определению 1, угол между плоскостями равен 90∘, значит, данные плоскости перпендикулярны. Теорема доказана. |
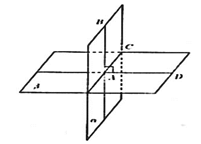
Теорема.Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.
| Доказательство. Пусть нам даны две плоскости α и β, пересекающиеся по прямой c. Плоскость γ перпендикулярна прямой c. Так как прямая c принадлежит плоскости α и плоскость γ перпендикулярна прямой c, то, по теореме 1, плоскости α и γ перпендикулярны. Так как прямая c принадлежит плоскости β и плоскость γ перпендикулярна прямой c, то, по теореме 1, плоскости β и γ перпендикулярны. Теорема доказана. |
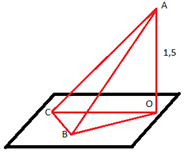
Задача 1. Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АО и две наклонные АВ и АС. Известно, что ∠OAB= ∠BAС = 60°, АО = 1,5 см. Найдите расстояние между основаниями наклонных.

Задача 2. Из точки D, не принадлежащей данной плоскости , проведены к ней две наклонные DA и DB, равные соответственно 18 см и 10 см. Сумма длин их проекций на плоскость равна 16 см. Найдите проекцию каждой из наклонных
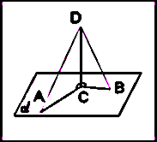
| . |
| Решение: | |
Задача 3. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.
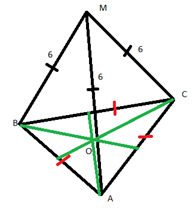

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
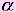 . Тогда по определению отрезки CА и CВ - соответственно проекции наклонных DA и DB. По условию CА+CВ=16 см. 2. Рассмотрим треугольник DСA, в нем угол С=90o; DA=18 м (по условию); По теореме Пифагора DC2=DA2-AC2; DC2=182-AC2; DC2=324-AC2;
. Тогда по определению отрезки CА и CВ - соответственно проекции наклонных DA и DB. По условию CА+CВ=16 см. 2. Рассмотрим треугольник DСA, в нем угол С=90o; DA=18 м (по условию); По теореме Пифагора DC2=DA2-AC2; DC2=182-AC2; DC2=324-AC2;