nd test, Micro II. Deadline – the Saturday, 11th.

2nd test, Micro II. Deadline – the Saturday, 11th.

Exercise 1. Consider the following game:

			Player 2
		L	C	R
	T	6, 5	0, 2	10, 2
Player 1	M	4, 3	2, 4	6, 3
	B	2, 4	0, 3	8, 6

a) Find all (pure and mixed) strategy Nash equilibria of this game. (Note: this game may be reduced by illuminating some strategies)

b) Assume this game is played twice. The players observe the outcome of the ﬁrst round before they choose their actions in the second round. The payoﬀs of the players for the whole game are the sum of the payoﬀs from the two rounds. Is there a pure-strategy subgame perfect Nash equilibrium in which the payoﬀ (8, 6) can be achieved in the ﬁrst round? Justify your answer!

Exercise 2. Consider infinitely repeated game with the following stage game:

			Player 2
		C	D
	C	2, 2	0, 3
Player 1	D	3, 0	1, 1

Is there a Nash equilibrium in which players play the following sequins of actions: {DC, CD, DC, CD, DC, CD, ….} in the inﬁnitely repeated game? (That is, actions of Player 1 are D in t = 0, 2, 6, … and C in t = 1, 3, 5…; actions of player 2 are C in t = 0, 2, 4… and C in t = 1, 3, 5,…). Justify your answer!

Exercise 3.In thefollowing signaling game find allpure strategyperfect Bayesian equilibria.

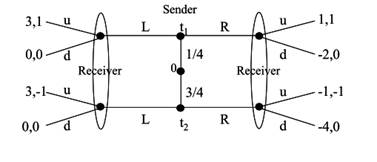
Exercise 4. The Nature chooses which game will be played: game A with p = 1/2, game B with p = 1/2. Player 1 has perfect information about which game is chosen. The following tables give the payoﬀs for each game:

		Player 2				Player 2
		U	D			U	D
Player 1	L	2, 2	0, 0	Player 1	L	0, 2	2, 0
	R	0, 0	2, -2		R	2, 0	0, -2

Game A Game B

Find all pure Bayesian Nash equilibria in this game of incomplete information, if they exist.

⇐ Предыдущая 1 2 3 45