Средняя длина свободного пробега молекулы

Средняя длина свободного пробега молекулы

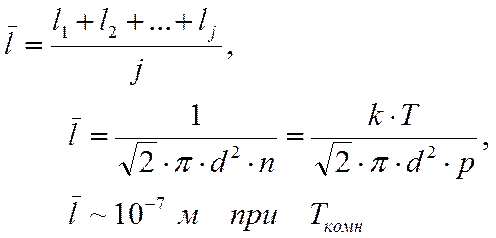
Оценим среднюю длину свободного пробега молекул воздуха. При нормальных условиях температура воздуха порядка комнатной, положим её равной

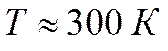а давление равно

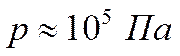Тогда

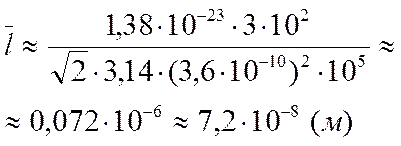Средняя длина свободного пробега позволяет определить среднюю арифметическую скорость молекулы

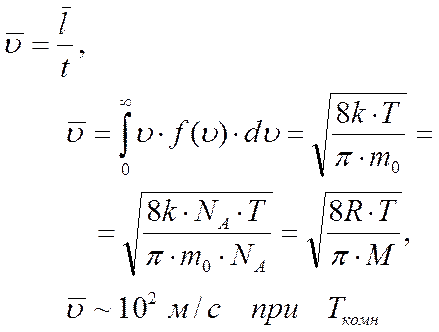
где f(u) – плотность вероятности (или функцией Максвелла), позволяющая вычислить среднюю арифметическую скорость.

Молекулы вещества при одной той же температуре движутся с разными скоростями. Распределение молекул по скоростям или кинетическим энергиям называется распределением Максвелла. Функция Максвелла (функция распределения молекул по скоростям) имеет вид (рис.):

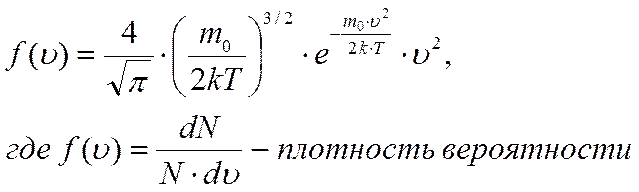
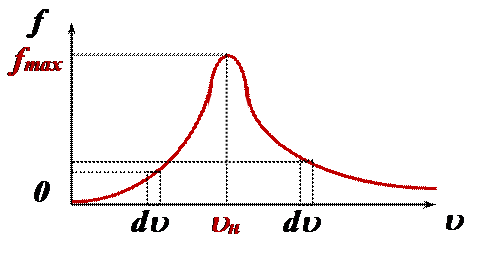Оно показывает, какая доля молекул от общего их числа (т. е. вероятность) движется со скоростями в заданном интервале значений скоростей:

1) доля медленных молекул мала

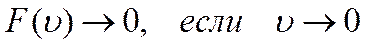
2) доля быстрых молекул мала

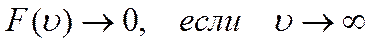
3) большинство молекул движется с наивероятнейшей скоростью

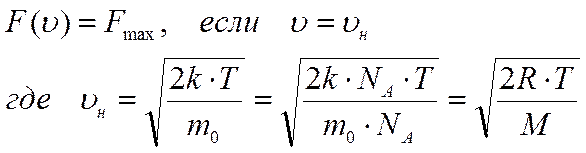
Распределение Максвелла:

- справедливо для равновесного состояния газа (с постоянной температурой), т. е. при отсутствии явлений переноса;

- не учитывает действие внешних потенциальных полей (поле силы тяжести).

В действительности же, полем силы тяжести нельзя пренебрегать. Оно влияет на концентрацию молекул в зависимости от удаления от поверхности Земли. Это влияние описывает распределение Больцмана – распределение молекул по потенциальным энергиям (рис.):

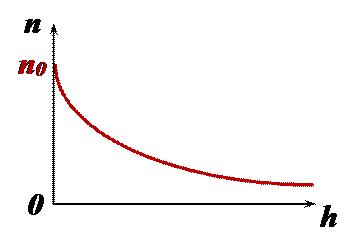
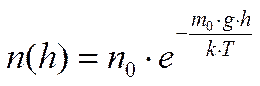
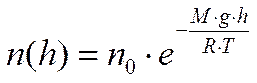
Поскольку

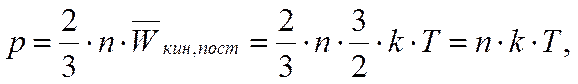
то справедлива и барометрическая формула

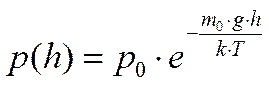
или

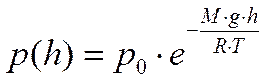
Распределение Больцмана и барометрическая формула выполняются:

- для равновесного состояния газа (с постоянной температурой), т. е. при отсутствии явлений переноса,

- для нижнего слоя атмосферы (тропосферы), имеющего толщину 10 - 11 км, поскольку в пределах этого слоя можно пренебречь зависимостью изменением ускорения свободного падения от высоты.

Вследствие закона сохранения энергии, оба распределения можно объединить в общее, которое называется распределением Максвелла – Больцмана, также справедливое для равновесного состояния газа.

Любая движущаяся молекула имеет среднюю кинетическую энергия молекулы. В случае только поступательного движения она равна:

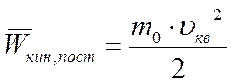
Эта энергия определяется по величине средней квадратичной скорости молекулы:

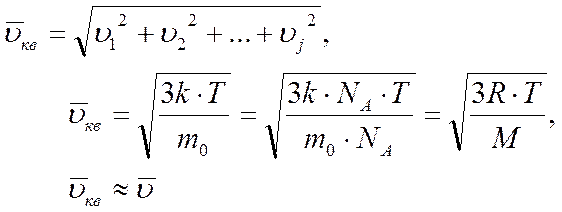
Эту скорость можно найти, в свою очередь, из основного уравнения МКТ. Основным уравнением молекулярно-кинетической теории строения вещества называют взаимосвязь макро- и микропараметров.

В частности, дляидеального газаосновное уравнение МКТ устанавливает количественное соотношение между давлением газа на стенки сосуда (макропараметр) и средней квадратичной скоростью поступательного движения молекулы (средней кинетической энергией молекулы) в качестве микропараметра:

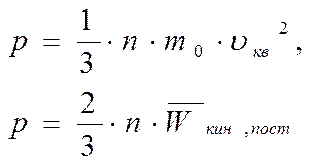
Молекулы газа в общем случае (реальный газ) могут двигаться не только поступательно, но и вращаться, а также существует колебательное движение атомов в молекуле. Поэтому число степеней свободы (возможных движений) равно

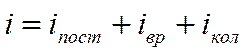
Теорема о равнораспределении средней кинетической энергии по степеням свободы: на каждую степень свободы приходится средняя кинетическая энергия, равная

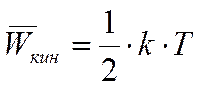
(k – постоянная Больцмана). Энергия молекулы, имеющей все степени свободы, равна

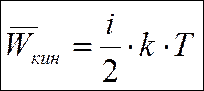
Частные случаи (рис. 4):

если молекула газа одноатомная, то

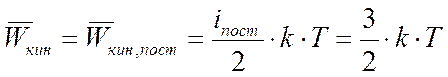1) если молекула газа «жёсткая» двухатомная, то

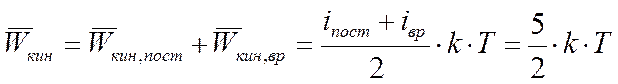
2) если молекула газа «жёсткая» трёх- и многоатомная, то

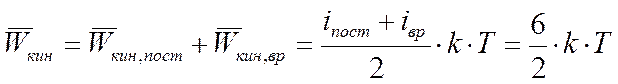
Из теоремы о равнорапределении энергии следует, что термодинамическая температура служит мерой кинетической энергии.

При охлаждении вещества сначала «замораживаются» поступательные степени свободы – газ переходит в жидкость, уменьшается число «кочующих» молекул, увеличивается – «осёдлых».

При дальнейшем охлаждении «замораживаются» вращательные степени свободы – жидкость превращается в твёрдое тело, частицы которого преимущественно колеблются около положений равновесия.

В пределе – при абсолютном нуле температуры – движение молекул прекращается с точки зрения классической физики.

На такой трактовке температуры была построена теоретическая шкала Кельвина – термодинамическая шкала:

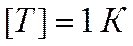
Практически применяют эмпирическую шкалу Цельсия:

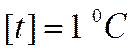
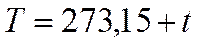
Однако даже при «абсолютном» нуле термодинамической температуры остаётся внутриатомное, внутриядерное и др. движения, описываемые квантовой физикой, и выводы классической физики на основе МКТ теряют прежний физический смысл.

⇐ Предыдущая 123 4 5 6 Следующая ⇒