Множества

АЛГЕБРА АБСТРАКТНАЯ

(общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых можно сочетать по различным правилам, получая в результате новые элементы, вне зависимости от конкретной природы самих элементов. В последние десятилетия абстрактная алгебра все глубже проникает в различные разделы математики, становясь неоценимым средством исследования в столь различных ее областях, как геометрия, топология, математический анализ и дифференциальные уравнения. Даже у социологов и аналитиков, работающих в сфере бизнеса, возникает необходимость в хотя бы поверхностном знакомстве с теорией матриц, являющейся частью абстрактной алгебры. Фактически в настоящее время сложилась такая ситуация, что наиболее важными являются не те достижения абстрактной алгебры, которые способствуют углублению наших знаний в самой этой области, а те, что предлагают новые средства исследования для других ветвей математики. Абстрактная алгебра оказалась полезной не только в математике. Ее средства и методы используются всюду, где возникает потребность в организации больших объемов данных. Абстрактная алгебра нашла применение при решении широкого круга проблем - от проектирования электронных схем до составления суточных графиков работы нефтеперегонных заводов, позволяющих максимизировать прибыль.

Множества

(С использованием материалов из Википедии)

Нынешние курсы математического анализа часто строятся на понятии множества. Например, в учебнике Ю. Г. Решетняк «Курс математического анализа», с. 12:

«Для нас множество будет одним из первичных математических понятий, не выражаемым через другие математические понятия. Обычно, говоря слово ,,множество‘‘, мы будем под этим понимать совокупность объектов произвольного рода, рассматриваемую как единое целое. Вместе с термином множество будут употребляться и его синонимы типа набор, система, совокупность и т. п. Например, можно говорить о множестве решений некоторого уравнения, о коллекции картин, хранящихся в музее, совокупности точек круга и т. д.

Объекты, составляющие то или иное множество, называются его элементами.

Множество считается заданным, если для любого объекта можно установить, является он элементом данного множества или нет».

В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов, «Математический анализ», с. 69:

«...при изучении вещественных чисел важным понятием являлось понятие множества. Подчеркнем, что множество мы рассматривали как начальное понятие, неопределенное через другие.

Мы рассмотрим множества произвольной природы или, как говорят, абстрактные множества. Это означает, что объекты, составляющие данное множество, или, как говорят, элементы данного множества уже не обязаны быть обязательно вещественными числами. Элементами абстрактного множества могут быть, например, функции, буквы алфавита, фигуры на плоскости и т. д.».

В. А. Зорич «Математический анализ»:

«Основные предпосылки канторовской (или, как условно говорят, "наивной") теории множеств сводятся к следующему:

1° множество может состоять из любых различных объектов;

2° множество однозначно определяется набором составляющих его объектов;

3° любое свойство определяет множество тех объектов, которые этим свойством обладают.

Если x — объект, P — свойство, P(x) — обозначение того, что x обладает свойством P, то через {x : P(x)} обозначают весь класс объектов, обладающих свойством P.

Объекты, составляющие класс или множество, называют элементами класса или множества.

Объедине́ние мно́жеств (также су́мма или соедине́ние)— множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств 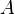и 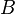обычно обозначается 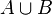, но иногда можно встретить запись в виде суммы .

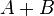Аксиома III (аксиома множества-суммы или объединения) Для любого множества а, содержащего по крайней мере один член, существует вполне определенное множество, членами которого являются в точности члены членов множества а.

Это множество называется множеством-суммой множества а, или объединением членов а. Оно обозначается через «∪а».
Итак, х ∈ ∪а оказывается верным, в том и только в том случае, если найдется такое z ∈ a (по крайней мере одно z), что х ∈ z.

Что такое 0? Прежде всего - это число, являющееся пустым множеством, т.е в котором нет элементов. Это множество есть неопределённость - стационарное бесконечное множество нулей. Таким образом 0 (как число) разделяет бесконечность и неопределённость.

· По правилам стандартной арифметики деление на число 0 запрещено.

· Частное от деления какого-либо числа, отличного от нуля, на нуль не существует, так как в этом случае никакое число не может удовлетворять определению частного^[1].

· Операции деления ненулевого числа на нуль не соответствует никакое действительное число. Однако число, отличное от нуля, можно разделить на число, как угодно близкое к нулю, и чем ближе делитель к нулю, тем больше будет частное. Поэтому, часто говорят, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов) и пишут:
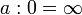, где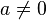
Смысл этого выражения состоит в том, что если делитель приближается к нулю, но не равен ему, а делимое остается равным a или приближается к нему, то частное неограниченно увеличивается (по модулю).

· Деление на ноль невозможно в пространстве комплексных чисел. В самом деле, если обозначить 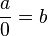, то по определению деления формально должно быть 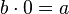, в то время как выражение 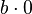, при любом комплексном 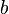, равно нулю. В математическом анализе возможно 7 неопределенных ситуаций, в 4 из которых формально присутствует ноль (он обозначает бесконечно малую величину):

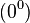
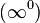
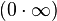
И вполне определенная ситуация, когда рассматривается предел бесконечно малой величины (справа или слева):

· Правый предел: 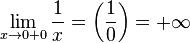_ или _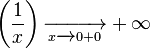

· Левый предел: 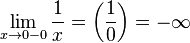_ или _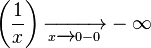

Если каждый элемент корабля был заменён хотя бы один раз, можно ли считать корабль прежним кораблём? В нашем организме каждый атом заменяется другим атомом того же элемента раз в 20-30 дней. Так можно ли считать, что человек остается тем же самым спустя 50 лет?

Этот парадокс возникает от того, что мы не дали определения ни кораблю, ни организму. Если корабль - множество именно этих деталей и никаких других, то при замене всех деталей мы несомненно имеем уже другой корабль. То же самое относится и к организму человека, если организм - то, что состоит именно из этих атомов.

· Но если корабль определить как систему, сущность которой определяется его свойствами как целого: весом, водоизмещением, скоростью, КПД и прочими характеристиками, то и при замене всех деталей аналогичными деталями корабль остается прежним. Свойства целого отличаются от свойств его частей и не сводятся к свойствам этих частей. Целое больше суммы его частей! Поэтому и в 50 лет человек остается самим собой, хотя 95% атомов его тела уже много раз за это время заменены другими, да и атомов в его теле становится больше, чем было в возрасте 10 лет.

· Так что не совсем прав был древний философ, заявив, что нельзя дважды войти в одну и ту же реку, так как вода в ней течет и все время молекулы ее в потоке заменяются. В этом случае неявно постулируется, что река - это сумма именно этих молекул воды и никаких других молекул воды. Но ведь это не так, ведь мы реку воспринимаем не как набор молекул воды, а как поток определенной глубины и ширины, с определенной скоростью течения, одним словом, река - это динамическая система, а не сумма своих частей.

Абстрактное множество.

В арифметике при сложении, 1+1 = 2. Но ведь это может быть и не всегда так. Если к одному яблоку прибавить еще одно яблоко, то получится 2 яблока. Но если на это посмотреть по-другому и считать не яблоки, а абстрактные множества, то сложив 2 множества, мы получим еще третье, состоящее из двух множеств. То есть в этом случае 1 + 1 = 3, а может быть 1+1=1 (два множества слились в одно).

· А сколько будет 1+1+1? В обычной арифметике получается 3. А если учесть все комбинации из 3 элементов сначала по 2, а потом по 3? Правильно, в этом случае 1+1+1=6 (три сочетания по 1 элементу, два сочетания по 2 элемента и 1 сочетание по 3 элемента).

Комбинаторная арифметика на первый взгляд кажется глупостью, но это так только с непривычки. В химии приходится считать сколько получится молекул воды, если взять 200 атомов водорода и 100 атомов кислорода. Получится 100 молекул воды. А если взять 300 атомов водорода и 100 атомов кислорода? Все равно получится 100 молекул воды и останется 100 атомов водорода. Итак, мы видим, что в химии находит себе применение иная арифметика . Подобные задачи имеют место и в экологии. Например, известно правило Либиха о том, что на растения оказывает влияние химический элемент в почве, который находится в минимуме. Даже если все другие элементы в большом количестве, растение сможет их усвоить столько, сколько позволяет элемент, находящийся в минимуме.

Г 60 Голубев В.К. Лекции по высшей математике .ч.1. Учебно-методическое пособие. Н. Новгород, 2008 г., 260с

Одним из основных понятий современной математики является понятие множества. Являясь исходным, множество не поддается точному определению и его смысл раскрывается лишь путем описания или пояснения на примерах.

Говорят, что любая совокупность объектов представляет собой абстрактное множество (множество), а предметы или объекты, его составляющие, называются элементами этого множества.

Множество принято обозначать заглавной буквой латинского алфавита, а элементы этого множества - строчными буквами.

Если задано некоторое множество A , то для всякого предмета a верно одно и только одно из утверждений: предмет a принадлежит множеству A (aÎA) или предмет a не принадлежит множеству A

(aÏA).

Очевидно, что элементами множества могут быть и множества. Например, каждый элемент множества живых организмов сам представляет собой множество живых клеток, его составляющих.

Множества могут содержать как конечное, так и бесконечное число элементов. Такие множества соответственно называются конечными и бесконечными.

Например, множество корней равнения x-1=0 - конечное, а множество натуральных чисел 1, 2, 3, 4, ... - бесконечное.

Рассмотрим далее множество действительных корней уравнения x²+1=0. Как нетрудно заметить, действительных корней это уравнение не имеет. Таким образом, мы приходим к понятию множества, не содержащего ни одного элемента.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается знаком Æ.

Может оказаться, что множества A и B состоят из одних и тех же элементов, т.е. каждый элемент множества A является элементом множества B и, наоборот, каждый элемент множества B является элементом множества A. В этом случае говорят, что множества A и B равны, т.е. A=B.

Например, множества (1,2,3,5) и (5,2,3,1) являются равными.

Далее, введем понятие подмножества некоторого множества. Если каждый элемент множества A принадлежит множеству B, то множество A называется подмножеством множества B, и записывается этот факт в виде

A Ì B; читается "A включено в B".

Если множество A не является подмножеством множества B, то это записывается в виде A Ë B; читается "A не включено в B".

1. Свойства множеств.

1. Если A=B, то AÌB и BÌA.

2. Если AÌB и BÌC, то AÌC

3. Если AÌB и BÌA, то A=B

4. AÌA при любом множестве A.

5. Пустое множество Æ является подмножеством любого множества.

2. Взаимно однозначное соответствие

Если каждому элементу множества A по некоторому закону можно поставить в соответствие один и только один элемент множества B и, наоборот, каждому элементу множества B можно поставить в соответствие один и только один элемент множества A, то такое соответствие между множествами A и B называется взаимно однозначным, а сами множества называются эквивалентными.

Например: Взаимно однозначное соответствие можно установить между множествами (1, 2, 3, 4,...) и (1, 1/2, 1/3, 1/4,...), между множеством точек отрезка длины 2 и множеством точек отрезка длины 5.

3. Операции над множествами

Над множествами возможно производить некоторые операции, т.е. по данным нескольким множествам строить новое множество.

а. Пересечение. Пересечением множеств A и B называется такое множество M, каждый элемент которого принадлежит как A, так и B.

Пересечение множеств A и B обозначается символом AÇB,

M=AÇB = {x|xÎA, xÎB}. Приведенную запись следует читать: "множество M, равное пересечению множеств A и B, состоит из элементов x, которые одновременно принадлежат множествам A и B".

Примеры:

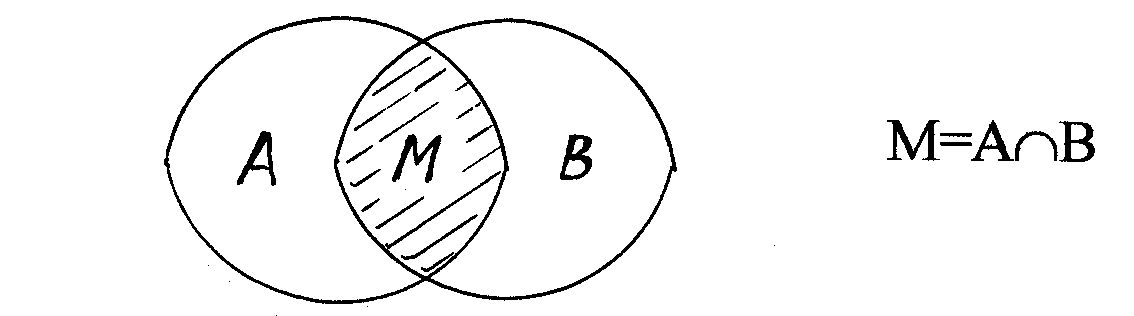
2. Если A - множество четных чисел, B - множество нечетных чисел, то AÇB=Æ. То есть множества A и B не пересекаются.

3. Если A={x | xÎ[0;5)}, B={x | x Î[2;7)}, то AÇB={x | xÎ[2;5)}.

4. Если A - множество всех ромбов, B - множество всех прямоугольников, то

AÇB - множество всех квадратов.

Задание. Изобразите схематически на плоскости взаимное расположение следующих множеств: R - множество вещественных чисел, Q -множество рациональных чисел, Z - множество целых чисел, Y - множество дробных чисел, N - множество натуральных чисел.

Замечание. Операция пересечения обладает свойствами

1. AÇB=BÇA 3. AÇA=A

2. AÇÆ=Æ 4. Если AÌB, то AÇB=A.

б. Объединение. Объединением множеств A и B называется множество M такое, каждый элемент которого принадлежит или множеству A, или множеству B.

Объединение множеств A и B обозначается символом AÈB, M=AÈB={x | xÎA или xÎB}. Приведенную запись следует читать:

"множество M, равное объединению множеств A и B, состоит из

элементов x, которые принадлежат либо множеству A, либо множеству B".

Примеры:

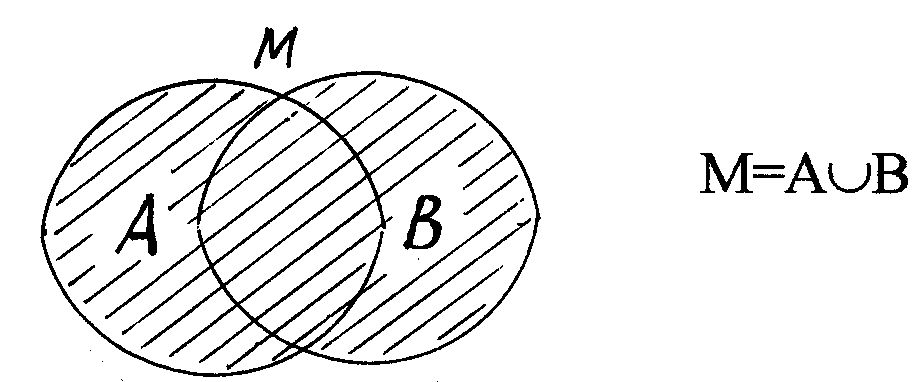
2. Если A - множество четных чисел, B - множество нечетных чисел, то AÈB - множество всех целых чисел - Z.

3. Если A={x | xÎ[0;5)}, B={x | xÎ[3;7)}, то M=AÈB={x | xÎ[0;7)}.

Замечание. Операция объединения множеств обладает свойствами:

1. AÈB=BÈA 2. AÈÆ=A

3. AÈA=A 4. Если AÌB, то AÈB=B

1. Перестановки

Далее всюду будем полагать, что нам задано конечное множество некоторых элементов. Элементами этого множества могут быть: люди, предметы, книги, молекулы и т.д.

Определение. Некоторая группа элементов заданного конечного множества называется соединением элементов данного множества.

Определение. Соединения из n элементов называются перестановками, если они содержат n элементов и отличаются друг от друга только их порядком.

Число перестановок из n элементов обозначается символом P_n или n!.

Теорема. Число перестановок из n элементов равно

n(n-1)(n-2)...3·2·1 ,т.е. P_nºn!=n(n-1)(n-2)...3·2·1 .

Пусть задано конечное множество из n элементов. Требуется выяснить: сколько будет упорядоченных соединений из данного множества , каждое из которых содержит n элементов ?

Очевидно, первый элемент соединения можно выбрать n способами, т.к. элементов множества всего n. Второй элемент можно выбрать уже (n - 1) способами, т.к. их осталось (n - 1) после выбора первого элемента. Процесс выбора продолжаем дальше.

Последний n-й элемент можно выбрать лишь одним способом, т.к. он остался один.

Таким образом, из множества, содержащего n элементов, можно составить n(n - 1)(n - 2). . .3·2·1 упорядоченных соединений из n элементов, т.е. перестановок.

Следовательно, P_n=n(n-1)(n-2)...3·2·1 .

12 Следующая ⇒