Теоретико-групповой анализ

Теоретико-групповой анализ

Для анализа магнитной структуры и оценки суперобменных взаимодействий в кристалле Ni_5.33Ta_0.67B₂O₁₀мы использовали простую модель непрямой связи [2,3], основанную на теории суперобменного взаимодействия Андерсона, Завадского [3] и Еремина. [4]. В рамках модели непрямой связи структура кристалла может быть охарактеризована следующими интегралами непрямой обменной связи с учетом заполнения отдельных катионных орбиталей и симметрий решетки непрямой связи J, где i и j - числа ij, неэквивалентные кристаллографические позиции для магнитных ионов. Рассчитанные обменные интегралы для Ni_5.33Ta_0.67B₂O₁₀ представлены в таблице.

Здесь b и c - параметры переноса электрона, представляющие собой квадраты коэффициентов смешения лиганд-катион для связи σ и π соответственно (значения этих параметров b = 0,02 и c = 0,01). U (Ni2 +) = 2,7 эВ - энергия возбуждения катион-лиганда; J (Ni 2+) = 2 эВ - интеграл межатомного обменного взаимодействия.

Таблица 1. Обменные взаимодействия.

J	углы	кол-во связей	J(K)
J₅	94,5 95,1
J₆	95,6 95,1
J₈	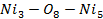98,7 94,7
J₁₁	93,6 98,2
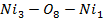
J₁₂	95,8 97,3
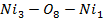
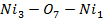
J₁₃	99,1 92,3
J₁₆	92,6 96,6
J₁₉	98,6 92,3
J₂₄	91,5 96,1
J₂₅	97,2 92,6
J₁	96,1 97,5
J₉	92,6 92,8
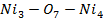
J₁₀	93,8 92,6
J₂₀	81,2 81,02
J₂₁	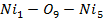81,7 81,1
J₂₂	96,3 96,3
J₂₃	97,4 97,4
J₂₆	96,1 96,7
J₃	120,6
J₂	115,8
J₄	118,7
J₇	119,8
J₁₄	165,2
J₁₅	162,6
J₁₇	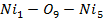166,1
J₁₈	163,3

Теоретический групповой анализ был выполнен для группы симметрииC 1 2/c 1 (15) monoclinic. Для случая, когда магнитная ячейка совпадает с кристаллографической. Магнитное представление строится для каждого элемента симметрии. Затем для этих магнитных представлений вычисляется разложение приводимых представлений на неприводимые представления, строится оператор проекции и вычисляются его собственные векторы.

Координаты атомов проиллюстрированы в таблице 2.

Таблица 2. Координаты атомов в системе Ni_5.33Ta_0.67B₂O₁₀

Атом

Тип обитали

Ni1

0.3749(5)

0.1265(8)

0.4991(8)

Ni2

0.2507(5)

0.0676(8)

0.2502(2)

Ni3

0.6090(4)

0.1874(8)

0.6092(2)

Ni4

0.1425(5)

0.0611(8)

0.3928(2)

Ni5

0,5

Ni6

0,75

0,25

0,5

Ni7

0.8132(12)

0,25

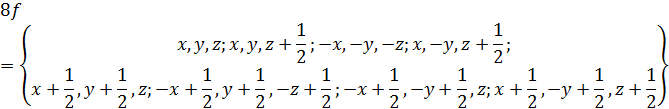
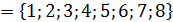
Таблица 3. Изменение положения атомов под действием элементов симметрии для 4a

Таблица 4. Изменение положения атомов под действием элементов симметрии для 4e

Таблица 5. Изменение положения атомов под действием элементов симметрии для 4c

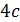
Таблица 6. Изменение положения атомов под действием элементов симметрии для 8f

Таблица 7. Собственные вектора неприводимых представлений

	τ1	τ2	τ3	τ4
8f	x y z	x y z	x y z	x y z
	-x -y z	-x -y z	x y -z	x y -z
	x y z	-x -y -z	x y z	-x -y -z
	-x -y z	-x -y z	x y -z	-x -y z
	x y z	x y z	x y z	x y z
	-x –y z	-x -y z	x y -z	x y -z
	x y z	-x -y -z	x y z	-x -y -z
	-x -y z	-x -y z	x y -z	-x -y z
4c	x y z	x y z	x y z	x y z
	-x -y z	-x -y z	x y -z	x y -z
	x y z	-x -y -z	x y z	-x -y -z
	-x -y z	x y -z	x y -z	-x -y z
4a	x y z	0 0 0	x y -z	0 0 0
	-x -y z	0 0 0	x -y -z	0 0 0
	x y z	0 0 0	x y z	0 0 0
	-x -y z	0 0 0	x -y -z	0 0 0
4e	x y z	0 0 0	x y z	0 0 0
	-x -y z	0 0 0	x -y -z	0 0 0
	x y z	0 0 0	x y z	0 0 0
	-x -y z	0 0 0	x -y -z	0 0 0

Возможен полный магнитный порядок: τ1 (z), τ3 (x, y) ферромагнитный, ферримагнитный. τ1 (x, y), τ3 (z) – антиферромагнитный.

для данной группы было проведено разложение по неприводимым представлениям для :

D(k=0)=33𝝉₁+33𝝉₂ +33𝝉₃ +33𝝉₄

Используя результат теоретико-групповой анализа, полученного ранее мы определили вероятные магнитные структуры, которые приведены в таблице 8

Таблица 8. Вычисленные значения энергий различных магнитоупорядоченных состояний.

8f1	8f2	8f3	8f4	4a	4c	4e	Выражение энергии через обменные интегралы Ji	Е(К)
↑	↑	↓	↓	↓	↓	↑	8J₁–16J₂–16J₃–16J₄+16J₅+16J₆–16J₇+16J₈+16J₉+16J₁₀+16J₁₁+16J₁₂+16J₁₃–16J₁₄–16J₁₅+16J₁₆+16J₁₇+16J₁₈+16J₁₉+16J₂₀+16J₂₁+ 8J₂₂+8J₂₃+16J₂₄+16J₂₅+8J₂₆	-611,2
↓	↑	↓	↓	↓	↓	↑	8J₁–16J₂–16J₃–16J₄–16J₅+16J₆–16J₇+16J₈+16J₉+16J₁₀+16J₁₁+16J₁₂+16J₁₃+16J₁₄+ 16J₁₅+16J₁₆+16J₁₇+16J₁₈+16J₁₉+16J₂₀+16J₂₁+ 8J₂₂+8J₂₃+16J₂₄+16J₂₅+8J₂₆	-483,2
↑	↓	↑	↑	↑	↓	↑	8J₁–16J₂–16J₃–16J₄+16J₅–16J₆+ 16J₇+16J₈+16J₉+16J₁₀–16J₁₁+16J₁₂+16J₁₃–16J₁₄–16J₁₅+16J₁₆+16J₁₇+16J₁₈+16J₁₉–16J₂₀+16J₂₁+ 8J₂₂+8J₂₃–16J₂₄+16J₂₅+8J₂₆	-459,2
↓↑	↑↓	↓↑	↓↑	↓↑	↑↓	↓↑	–8J₁+16J₂–16J₃–16J₄–16J₈+16J₉+16J₁₀+16J₁₁+16J₁₂+16J₁₃+ 16J₁₅+16J₁₆–16J₁₇–16J₁₈+16J₁₉+16J₂₀–16J₂₁+ 8J₂₂+8J₂₃+16J₂₄–16J₂₅+8J₂₆	-454,4
↓	↓	↑	↑	↑	↑	↑	8J₁–16J₂–16J₃–16J₄–16J₅–16J₆+ 16J₇+16J₈+16J₉+16J₁₀+16J₁₁–16J₁₂–16J₁₃–16J₁₄–16J₁₅–16J₁₆–16J₁₇–16J₁₈–16J₁₉–16J₂₀+16J₂₁+ 8J₂₂+8J₂₃+16J₂₄+16J₂₅+8J₂₆	-430,4
↓↑	↑↓	↓↑	↓↑	↑↓	↑↓	↑↓	–8J₁+16J₂–16J₃–16J₄+16J₈+16J₉+16J₁₀+16J₁₁+16J₁₂+16J₁₃+ 16J₁₅+16J₁₆+16J₁₇+16J₁₈+16J₁₉+16J₂₀+16J₂₁+ 8J₂₂+8J₂₃+16J₂₄+16J₂₅+8J₂₆	-390,4
↑	↓	↑	↓	↑	↑	↑	8J₁–16J₂–16J₃–16J₄–16J₅–16J₆+16J₇–16J₈+16J₉+16J₁₀+16J₁₁+16J₁₂+16J₁₃+16J₁₄+ 16J₁₅+16J₁₆–16J₁₇–16J₁₈+16J₁₉+16J₂₀–16J₂₁+ 8J₂₂+8J₂₃+16J₂₄–16J₂₅+8J₂₆	-366,4

1. K. Bluhm, Hk. Miller-Buschbaum, Solid State Ionics 43, 1-5 (1990)

2. O. A. Bayukov, A. F. Savitskii 1994 Fiz. Tverd. Tela 36 1923

3. P. W. Anderson 1959 Phys. Rev. 115 2

4. M. V. Eremin 1982 Fiz. Tverd. Tela 24 423

5. R. J. Goff, A. J. Williams, J. P. Attfield, Phys. Rev. B 70,014426 (2004)

6. P. Bordet, E. Suard, Phys. Rev. B 79, 144408 (2009)

7. A. K. Zvezdin, S. S. Krotov, A. M. Kadomtseva, G. P. Vorob’ev,Y. F. Popov, A. P. Pyatakov, L. N. Bezmaternykh, E. Popova, JETP Lett. 81, 272 (2005)

8. L. N. Bezmaternykh, S. N. Sofronova, N. V. Volkov, E. V. Eremin,O. A. Bayukov, I. I. Nazarenko, D. A. Velikanov, Phys. Status Solidi B 249, 1628 (2012).

⇐ Предыдущая 12