Произведение синусов и косинусов, вывод формул, примеры.

Произведение синусов и косинусов, вывод формул, примеры.

Изучение основных формул тригонометрии продолжаем формулами произведения синусов, косинусов и синуса на косинус. Эти формулы являются в определенном смысле обратными формулам суммы синусов и косинусов, то есть, позволяют от произведения синусов и косинусов углов 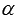и 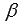перейти к сумме или разности синусов и косинусов углов 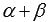и .

В этой статье мы рассмотрим следующие формулы: произведение синусов, произведение косинусов и произведение синуса на косинус, покажем их вывод, а также приведем примеры их использования.

Список формул

Запишем по порядку формулы произведения синусов, косинусов и синуса на косинус.

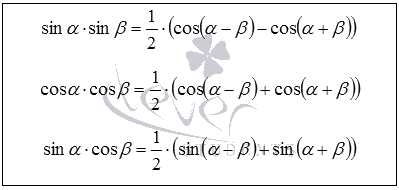
Эти формулы справедливы для любых углов 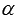и .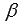

Озвучим формулировки данных формул произведения:

Произведение синусов углов 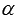и 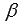равно полуразности косинуса угла и косинуса угла .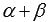
Произведение косинусов углов 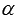и 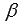равно полусумме косинуса разности углов 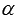и 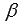и косинуса суммы этих углов.
Произведение синуса угла 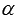и косинуса угла 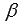равно полусумме синуса разности углов 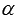и 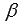и синуса суммы этих углов.

К началу страницы

Вывод формул

Формулы произведения синусов, косинусов и синуса на косинус можно вывести, основываясь на формулах сложения, а также на следующем свойстве равенств: если к левой и правой части верного равенства прибавить соответственно левую и правую части другого верного равенства, то получится верное равенство.

Для вывода формул произведения синусов и косинусов нам потребуются формулы косинуса суммы и косинуса разности вида 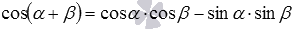и .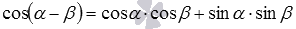

Сложив эти равенства, получаем , откуда следует, что 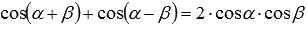и 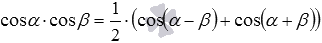. Так доказана формула произведения косинусов.

Если же формулу косинуса суммы переписать как 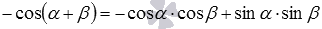, после чего к этому равенству прибавить равенство 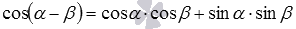, то легко получается формула произведения синусов вида .

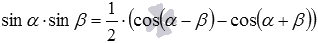Для вывода формулы произведения синуса на косинус достаточно сложить левые и правые части формул синуса суммы 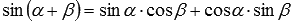и синуса разности 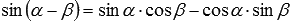. Имеем 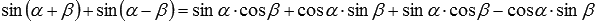, откуда следует, что .

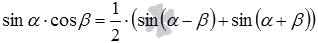Так мы вывели формулы произведения синусов, косинусов и синуса на косинус.

К началу страницы

12 Следующая ⇒