Квазианалитический расчет критической длины основной волны П-волновода с выступами на ребре

Квазианалитический расчет критической длины основной волны П-волновода с выступами на ребре

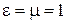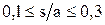Рассчитать нормированную критическую длину основной волны ПВВР ( ) при и 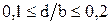. Шаг изменения 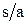и 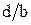составляет 0,1. По результатам расчетов постройте график зависимости нормированной критической длины основной волны ПВВР от s/a при различных d/b. Значения 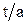=0,4 и 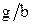=0,5, b/a=0,2. (Вариант 8)

Рассчитаем критическую длину основной волны для ПВВР в программе MATHCAD:

Решение:

Найдем индуктивность контура:

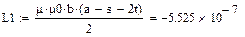
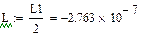Найдем емкость контура:

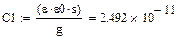
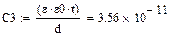
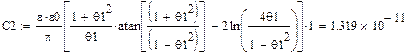
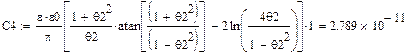Найдем критическую длину основной волны ПВВР:

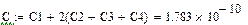
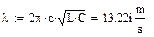
Дальше будем писать только результат длины волны.

Для s/a=0,2, d/b=0,1

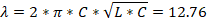
Для s/a=0,3, d/b=0,1

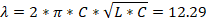
Для s/a=0,1, d/b=0,2

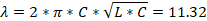
Для s/a=0,2, d/b=0,2

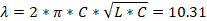
Для s/a=0,3, d/b=0,2

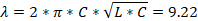
На основании проведённых квазианалитических расчётов построим зависимость нормированной критической длины основной волны ПВВР от s/a при различных d/b:

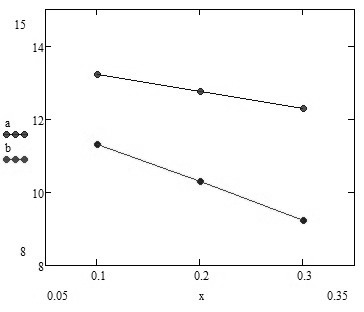
y- d/b =0.1 z - d/b=0/2

Рисунок 3- График квазистационарного расчета критической длины основной волны П-волновода с выступами на ребре

Заключение

В ходе работы был проведен квазианалитический расчет критической длины основной волны ПВВР и НВВР при различных значениях геометрических размеров и параметров диэлектрического заполнения и построен график зависимости длины нормированной критической длины основной волны ПВВР от s/a при различных d/b.

Таким образом, применение рассмотренного в настоящей работе комбинированного численно-аналитического подхода позволило оценить влияние прямоугольных выступов в ПВВР на поперечную электрическую компоненту и критическую длину основной волны. Кроме того, полученная на основе МЭС квазианалитическая зависимость критической длины основной волны ПВВР от размеров поперечного сечения и электрофизических параметров диэлектрического заполнения позволила существенно снизить вычислительные затраты. Необходимо также отметить, что рассмотренные выше квазианалитические выражения могут быть с успехом адаптированы для расчета критической длины основной волны ПВВР с неоднородным диэлектрическим заполнением.

⇐ Предыдущая 1 234 Следующая ⇒