- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Исследование квазианалитической критической длины основной волны П- Н- волновода с выступами на ребрах
Введение
В данной работе мы осваиваем комбинированные подходы к расчетам критической длины основной волны волновода с выступами на ребрах и структуры поля.
П-волноводы с выступами на ребрах, электродинамические свойства которых обычно анализируют одновременно, относятся к линиям передачи сложных сечений, позволяющим изменять распределение электрической компоненты в поперечном сечении. Эта особенность обусловливает перспективность применения ПВВР в качестве базовых элементов при конструировании СВЧ-устройств различного назначения. Поскольку в большинстве случаев такие устройства, как правило, функционируют в одноволновом режиме, важный практический интерес представляет исследование влияния выступов в ПВВР на критическую длину 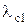 основной волны.
основной волны.
Исследование квазианалитической критической длины основной волны П- Н- волновода с выступами на ребрах
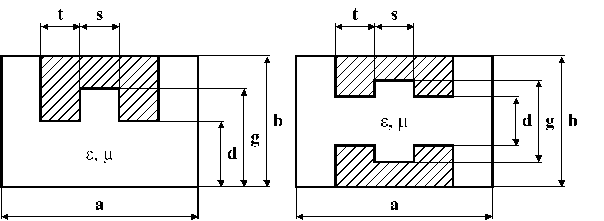
П- (ПВВР) (рис. 1 а) и Н- (НВВР) (рис. 1 б) волноводы с выступами на ребрах, электродинамические свойства которых обычно анализируют одновременно, относятся к линиям передачи сложных сечений, позволяющим изменять распределение электрической компоненты в поперечном сечении. Эта особенность обусловливает перспективность применения ПВВР и НВВР в качестве базовых элементов при конструировании СВЧ-устройств различного назначения. Поскольку в большинстве случаев такие устройства, как правило, функционируют в одноволновом режиме, важный практический интерес представляет исследование влияния выступов в ПВВР и НВВР на критическую длину 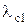 основной волны.
основной волны.
|
а б Рисунок 1 - Поперечные сечения ПВВР (а) и НВВР (б) |
Определить критическую длину основной волны ПВВР и НВВР на основе точного аналитического решения внутренней краевой задачи электродинамики не удается из-за сложной формы границ волноводов. Поэтому приходится прибегать к приближенным методам расчета, среди которых, прежде всего, необходимо отметить численные подходы [1-7]: метод конечных элементов (МКЭ), метод конечных разностей, метод частичных областей, альтернирующий метод Шварца, вариационный метод, метод интегральных уравнений, метод R-функций и некоторые другие. Основным достоинством численных методов является их универсальность, а недостатками – частный характер результатов, значительные трудности математического и вычислительного характера. Кроме того, первое приближение этих методов достаточно часто дает результат с большой погрешностью.
В инженерной практике хорошо зарекомендовал себя метод эквивалентных схем (МЭС), основанный на замене реальной электродинамической системы эквивалентной цепью с сосредоточенными параметрами. К достоинствам МЭС относятся наглядность, сравнительная простота вычислений, возможность описать различные линии передачи ограниченным количеством разновидностей эквивалентных схем и выявить общие закономерности их функционирования. Выбор эквивалентной схемы зависит от физических свойств замещаемой структуры и используемого подхода. Точность расчета МЭС зависит от точности определения параметров эквивалентной схемы, которые могут быть либо оценены качественно, либо рассчитаны методами теории поля.
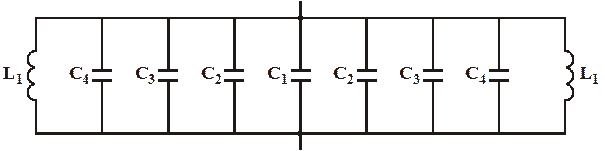
Критическую длину основной волны ПВВР и НВВР с однородным диэлектрическим заполнением можно квазианалитически рассчитать исходя из замены анализируемой электродинамической системы эквивалентной схемой из сосредоточенных индуктивностей и емкостей (рис. 2)
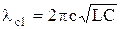 , (1)
, (1)
где 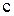 – скорость света;
– скорость света; 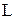 и
и 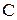 – результирующие индуктивность и емкость эквивалентного колебательного контура.
– результирующие индуктивность и емкость эквивалентного колебательного контура.
Индуктивность контура для расчета критической длины основной волны может быть представлена в виде
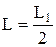 , (2)
, (2)
где 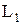 – индуктивность боковой секции ПВВР или НВВР, вычисляемая по формуле
– индуктивность боковой секции ПВВР или НВВР, вычисляемая по формуле
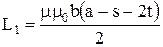 , (3)
, (3)
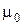 – магнитная постоянная;
– магнитная постоянная; 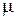 – относительная магнитная проницаемость заполнения.
– относительная магнитная проницаемость заполнения.
Емкость контура в этом случае определяется выражением
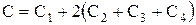 , (4)
, (4)
где 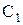 и
и 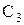 – электростатические емкости;
– электростатические емкости; 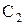 и
и 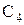 – краевые емкости.
– краевые емкости.
|
Рисунок 2 - Эквивалентная схема для расчета критической длины основной волны ПВВР и НВВР |
Электростатические емкости 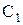 и
и 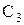 можно рассчитать по формуле плоского конденсатора из соотношений:
можно рассчитать по формуле плоского конденсатора из соотношений:
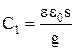 ; (5)
; (5)
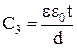 , (6)
, (6)
где 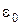 – электрическая постоянная;
– электрическая постоянная; 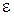 – относительная диэлектрическая проницаемость заполнения.
– относительная диэлектрическая проницаемость заполнения.
Краевые емкости 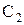 и
и 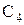 вычисляются по формулам
вычисляются по формулам
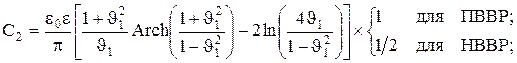 (7)
(7)
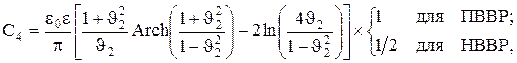 (8)
(8)
где 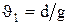 и
и 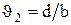 .
.
Таким образом, применение квазианалитического подхода на основе МЭС позволяет в первом приближении оценить влияние геометрических размеров и электрофизических параметров диэлектрического ПВВР и НВВР на критические длины их основных волн.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|