Тема: Прямые и плоскости в пространстве.

Тема: Прямые и плоскости в пространстве.

Задача № 1

Точка A лежит в плоскости α , ортогональная проекция отрезка AB на эту плоскость равна 1, AB = 2. Найдите расстояние от точки B до плоскости α.

Решение:

Пусть B₁– ортогональная проекция точки B на плоскость α . Тогда BB₁– перпендикуляр к плоскости α , AB₁– ортогональная проекция отрезка AB на плоскость α , а расстояние от точки B до плоскости α равно длине отрезка BB₁. Прямая BB₁перпендикулярна плоскости α , поэтому треугольник ABB₁– прямоугольный. По теореме Пифагора

BB₁ = = = .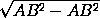

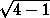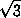Ответ: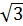

Задача № 2

Высота прямоугольного треугольника ABC, опущенная на гипотенузу, равна 9.6. Из вершины C прямого угла восставлен к плоскости треугольника ABC перпендикуляр CM, причем CM = 28. Найдите расстояние от точки M до гипотенузы AB.

Решение:

Пусть CK - высота данного прямоугольного треугольника. Тогда MK - наклонная к плоскости треугольника ABC, а CK - ортогональная проекция этой наклонной на плоскость треугольника ABC. Так как CK 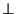AB, то по теореме о трех перпендикулярах MK 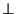AB. Значит, длна отрезка MK равна расстоняию от точки M до прямой AB. Из прямоугольного треугольника MCK по теореме Пифагора находим, что

MK = = = =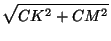

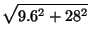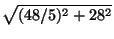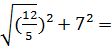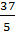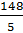=4 4* = =29,6

Ответ: 29,6

Тема: Комбинаторика

1.В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Решение:

Капитаном может стать любой из 11 футболистов. После выбора капитана на роль его заместителя могут претендовать 10 оставшихся человек. Таким образом, всего есть 11·10 = 110 разных вариантов.

Ответ: 110 способами

2.На танцплощадке собрались N юношей и N девушек. Сколькими способами они могут разбиться на пары для участия в очередном танце?

Решение:

"Зафиксируем" девушек. Тогда разбиение на пары определяется перестановкой юношей.

Ответ: N! способами.

12 Следующая ⇒