Теоретические основы эксперимента

Лабораторная работа №4

“Определение коэффициента теплоотдачи при свободной конвекции вертикальной трубы”

Цель работы: изучение способов опытного определения коэффициента теплоотдачи и получения критериальных уравнений при естественной конвекции. Приобретение навыков постановки технических экспериментов, более глубокое изучение теории процесса теплообмена.

1 Теоретические основы эксперимента

Процесс переноса тепла между твердой стенкой и омывающей ее жидкостью называется конвективным теплообменом или теплоотдачей. Тепло при этом будет переноситься совокупным воздействием теплопроводности и конвекции. В зависимости от причины, вызывающей течение жидкости, движение может быть свободным и вынужденным. Свободными называются течения, происходящие вследствие воздействия неоднородного поля массовых сил, приложенным к элементам массы внутри рассматриваемой системы и обусловленные внешними полями (гравитационными, магнитными, электрическими). Свободное движение под действием гравитационного поля при неравномерном распределении плотности жидкости называется свободным гравитационным движением или свободной гравитационной конвекцией. Перенос тепла жидкостью при ее свободном движении называется теплоотдачей при свободной конвекции. Неоднородность распределения плотности при этом может быть вызвана самыми различными причинами: неоднородность распределения температуры, различной по объему концентрации некоторого компонента в смеси, наличием фаз с различной плотностью.

Вынужденным считается движение жидкости, вызванное посредством подвода к жидкости механической энергии от посторонних устройств – насоса, компрессора, вентилятора. Вынужденное течение почти всегда сопровождается свободным. Причем влияние последнего тем больше, чем больше перепад плотности в отдельных элементах объема жидкости.

Интенсивность процесса обмена теплом определяется коэффициентом теплоотдачи. Осредненный по поверхности коэффициент теплоотдачи может быть рассчитан по формуле Ньютона

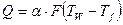, (1.1)

где 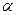- коэффициент теплоотдачи;

F – площадь поверхности;

T_W – температура поверхности;

T_f – температура омываемой среды.

С физической точки зрения коэффициент теплоотдачи представляет количество тепла, переданное в единицу времени через единицу поверхности при температурном напоре 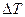в один градус.

Процесс теплоотдачи неразрывно связан с характером течения жидкостей. Характер движения теплоносителя около стенки зависит от формы поверхности ее положения в пространстве и направления теплового потока. На рисунке 1.1 показана картина движения теплоносителя около охлаждаемой вертикальной стенки (а),около охлаждаемых (б, в)и около нагреваемых горизонтальных поверхностей (г, д).

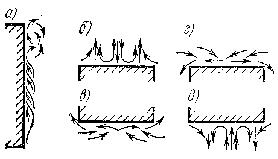
Рисунок 1.1 – Движение теплоносителя

Движение теплоносителя вдоль охлаждаемой вертикальной стенки в нижней части имеет ламинарный характер, выше — переходный, а затем - вихревой. В случае нагреваемой стенки теплоноситель перемнется сверху вниз, и характер течения изменится в той же последовательности. Режим течения определяется главным образом температурным напором, с увеличением которого сокращается длина участка, занятого ламинарным потоком, и увеличивается зона вихревого движения. На участке ламинарного движения коэффициент теплоотдачи уменьшается в соответствии с увеличением толщины ламинарного слоя теплоносителя. В зоне вихревого движения коэффициент теплоотдачи имеет практически одинаковое значение для всей поверхности.

Характер движения теплоносителя около плоских горизонтальных поверхностей зависит от их расположения и направления теплового потока. При картине движения, отвечающей схемам в и г, поверхность стесняет движение теплоносителя, и потому теплообмен протекает менее интенсивно, чем в случаях б и д.

Характер свободного движения теплоносителя в ограниченном пространстве зависит от формы и взаимного расположения поверхностей, образующих прослойку, а также от расстояния между ними.

Движение теплоносителя по-разному протекает в замкнутых и открытых прослойках.

На рисунке 1.2 рассмотрены два случая теплоотдачи при свободном движении теплоносителя в ограниченном пространстве: теплоотдача в замкнутой прослойке (а) и теплоотдача в открытом зазоре при одинаковой температуре стенок, образующих зазор (б).

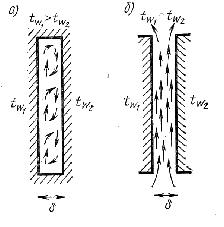
Рисунок 1.2 – Теплоотдача при свободном движении

теплоносителя в ограниченном пространстве

При теплоотдаче в замкнутом пространстве перенос теплоты осуществляется одним и тем же теплоносителем, который циркулирует между горячей и холодной стенками, образуя замкнутые контуры. В этом случае трудно отделить теплоотдачу около охлаждаемой и нагреваемой поверхностей. Поэтому процесс теплообмена в замкнутой прослойке оценивают в целом, определяя плотность теплового потока формулой теплопроводности

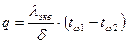, (1.2)

где 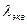— эквивалентный коэффициент теплопроводности;

d — толщина прослойки.

Эквивалентный коэффициент теплопроводности учитывает интенсивность циркуляции в прослойке и определяется через коэффициент теплопроводности теплоносителя формулой

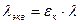, (1.3)

где 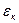— коэффициент конвекции.

Опытное исследование теплоотдачи в замкнутом пространстве показало, что независимо от формы прослойки коэффициент конвекции можно определить из уравнения

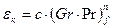(1.4)

в котором с и п зависят от величины произведения 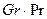. При 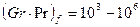значения с = 0,105 и n = 0,3, при 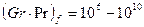с = 0,4 и п = 0,2. При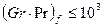 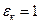, т. е. циркуляция отсутствует, и теплота передается только теплопроводностью.

В уравнении (1.4) за определяющую выбрана средняя температура теплоносителя, равная полусумме температур стенок, а за определяющий размер — толщина прослойки d.

Опытное изучение теплоотдачи в открытом зазоре при свободном движении воздуха между вертикальными стенками, имеющими одинаковую температуру, показало, что существует критическая величина зазора, при которой теплообмен достигает наибольшей интенсивности. При зазорах меньше критического интенсивность теплообмена резко ухудшается, а при зазорах больше критического — остается практически неизменной. При теплоотдаче в воздухе критическая величина зазора определяется из равенства

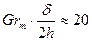, (1.5)

где d — расстояние между стенками;

h — высота стенки.

При подсчете числа Gr за определяющий размер принята половина расстояния между стенками.

Максимальная интенсивность теплообмена достигается при условиях, когда толщина пограничного слоя становится равной половине расстояния между стенками.

Теплоотдача в зазоре протекает более интенсивно, чем при свободном движении около одиночной пластины. При расстояниях между вертикальными стенками, близких к критическим ( 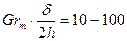), опытные данные по теплоотдаче удовлетворительно описываются уравнением

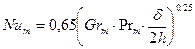(1.6)

Определяющий размер здесь выбирается так же, как в уравнении (1.5).

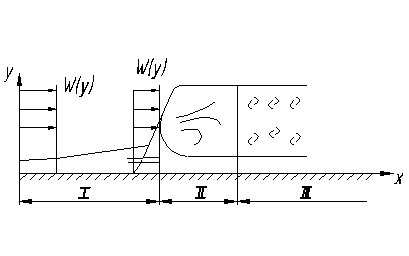
При некоторой скорости, определенной для каждого конкретного рассматриваемого случая движения жидкости, происходит изменение режима. Скорость, при которой наступает процесс изменения режима течения, носит название критической скорости. Переход из ламинарного в турбулентный режим течения осуществляется не мгновенно, а на некотором участке, режим течения на котором носит название переходного, участок II (рисунок 1.3) На участке III имеет место турбулентное течение.

12 3 4 5 6 7 Следующая ⇒