Ш. Законы распределения дискретных случайных величин.

Ш. Законы распределения дискретных случайных величин.

Биномиальный закон распределения. Пусть производится 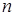независимых испытаний, в каждом из которых событие 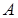может появиться или не появиться. Вероятность появления события 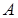во всех испытаниях постоянна и равна .

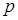Рассмотрим в качестве дискретной случайной величины 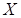число появлений события 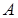в этих испытаниях. Найдем закон распределения случайной величины 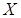. Для этого надо определить возможные значения 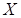и их вероятности. Возможные значения 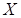: 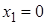, , 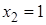, 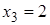…, 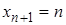. Вероятности этих возможных значений определяются по формуле Бернулли

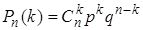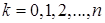, . (22)

Эта формула является аналитическим выражением искомого закона распределения.

Распределение вероятностей, определяемое формулой Бернулли, называется биномиальным, так как правую часть равенства (22) можно рассматривать как общий член разложения бинома Ньютона:

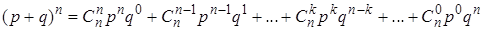Таблица биномиального закона имеет вид:

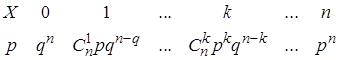. (23)

Пример 3. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины 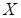– числа выпадений герба.

Решение. Событие 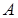– выпадение герба при одном броске монеты. Вероятность появления события 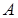при каждом броске постоянна и равна 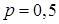. Поэтому случайная величина 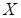– число выпадений герба – распределена по биномиальному закону. Найдем закон распределения этой случайной величины по формулам (23):

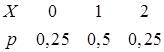Математическое ожидание дискретной случайной величины, распределенной по биномиальному закону, равно произведению числа испытаний на вероятность появления события в одном испытании:

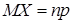. (24)

Дисперсия дискретной случайной величины, распределенной по биномиальному закону, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании,

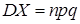. (25)

Закон распределения Пуассона. В случаях, когда 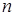велико, а вероятность 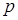мала, используется асимптотическая формула Пуассона. Найдем вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события 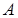очень мала, это событие наступит ровно 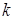раз. При этом предполагается, что произведение 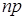сохраняет постоянное значение 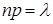. По формуле Бернулли вычислим вероятность

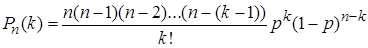но 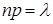, , 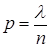тогда

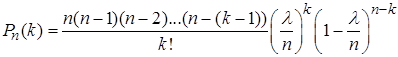Учитывая, что 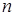имеет очень большое значение, вместо 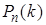найдем 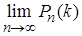. Так как произведение 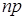постоянно и равно 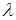, то при ,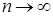

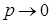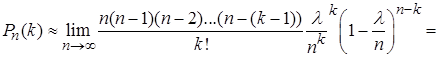
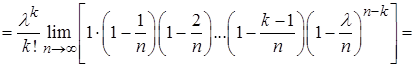
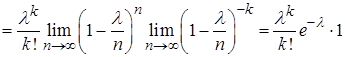Формула

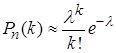(26)

выражает закон распределения Пуассона вероятностей массовых ( 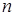велико) и редких ( 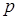мало) случайных событий.

Числовые характеристики дискретной случайной величины, распределенной по закону Пуассона:

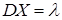, . (27)

Геометрический закон распределения. Пусть производятся независимые испытания, в каждом из которых вероятность появления события 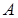равна 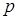( 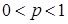). Испытания заканчиваются, как только появится событие 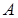, то есть если событие 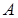появилось в 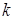-ом испытании, то в предыдущих 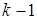испытании оно не появилось.

Обозначим через дискретную случайную величину – число испытаний, которые надо провести до первого появления события 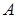. Возможные значения : 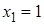, , 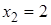…, 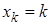. Вероятность того, что в первых 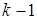испытаниях событие 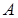не наступило, а в 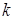-ом испытании появилось, по теореме умножения вероятностей независимых событий,

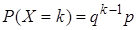. (28)

Полагая в формуле (28) 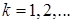, получим бесконечно убывающую геометрическую прогрессию с первым членом 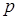и знаменателем ( ):

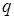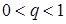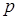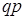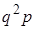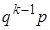, , , …, , … (29)

Поэтому распределение (28) называется геометрическим.

Сумма вероятностей (28) является суммой членов бесконечно убывающей геометрической прогрессии (29):

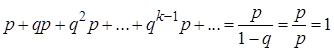Числовые характеристики дискретной случайной величины, распределенной по геометрическому закону:

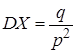, . (30)

Гипергеометрический закон распределения. Для того чтобы дать определение гипергеометрического распределения, рассмотрим задачу. Пусть в партии из 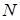изделий 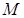стандартных ( 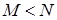). Из партии случайным образом отбирают 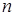изделий. Каждое изделие быть извлечено с одинаковой вероятностью. Отобранное изделие перед отбором следующего не возвращается в партию. Поэтому формула Бернулли здесь неприменима.

Обозначим случайную величину – число 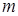стандартных изделий среди 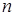отобранных. Возможные значения случайной величины : 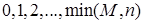. Вероятность того, что ,

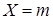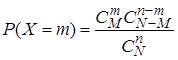. (31)

Эта формула определяет распределение вероятностей, которое называется гипергеометрическим. Это распределение определяется тремя параметрами , , .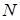

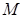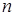Числовые характеристики дискретной случайной величины, распределенной по гипергеометрическому закону:

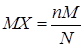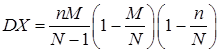, . (32)

⇐ Предыдущая 12