Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать формулы сокращенного умножения.

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

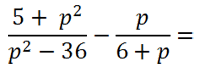
В первой алгебраической дроби знаменатель «(p² − 36)». Очевидно, что к нему можно применить формулу разности квадратов.

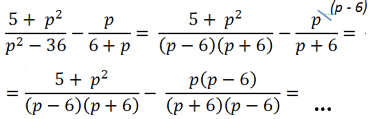
После разложения многочлена «(p² − 36)» на произведение многочленов
«(p + 6)(p − 6)» видно, что в дробях повторяется многочлен «(p + 6)». Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6)».

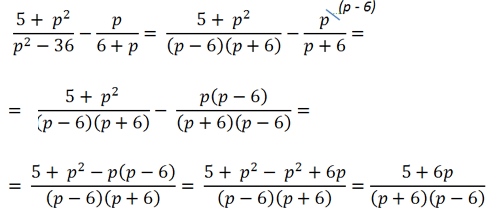
Важно!

Прежде чем приводить многочлены к общему знаменателю, попытайтесь использовать формулы сокращённого умножения или вынесение общего множителя за скобки.

Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.

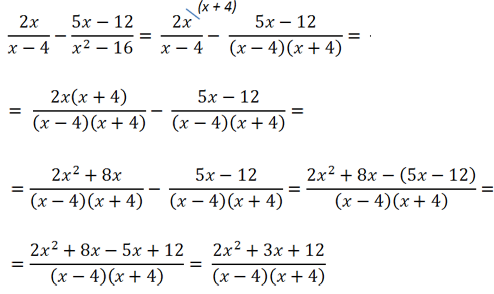
Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

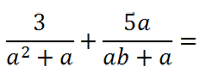
На первый взгляд одинаковых многочленов в обеих дробях нет.

Вынесем общий множитель «а» за скобки в обоих знаменателях.

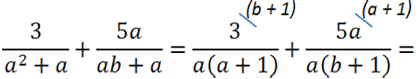
После вынесения общего множителя «а» за скобки, в обоих знаменателях появился одинаковый одночлен «а». Значит, общий знаменатель для обеих дробей будет выглядеть так: «а(а + 1)(b + 1)».

⇐ Предыдущая 1 234 Следующая ⇒