
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Приведение алгебраических дробей к общему знаменателю
Приведение алгебраических дробей к общему знаменателю
Рассмотрим другой пример. Требуется сложить алгебраические дроби.
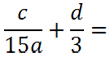
В таком виде сложить дроби нельзя, так как у них разные знаменатели.
Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.
Правила приведения алгебраических дробей к общему знаменателю очень похожи на правила приведения к общему знаменателю обыкновенных дробей. .
В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.
Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.
- Работаем с числовыми коэффициентами. Определяем НОК (наименьшее общее кратное) для всех числовых коэффициентов.
- Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
- Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
- Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.
Вернемся к нашему примеру.
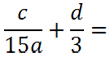
Рассмотрим знаменатели «15a» и «3» обеих дробей и найдем для них общий знаменатель.
- Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка делится на каждый числовый коэффициент). Для «15» и «3» — это «15».
- Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях. В знаменателях «15a» и «5» есть только
один одночлен — «а». - Перемножим НОК из п.1 «15» и одночлен «а» из п.2. У нас получится «15a». Это и будет общим знаменателем.
- Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a»?».
Рассмотрим первую дробь. В этой дроби и так знаменатель «15a», значит, ее не требуется ни на что умножать.
Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3», чтобы получить «15a»?» Ответ — на «5a».
При приведении к общему знаменателю дроби умножаем на «5a» и числитель, и знаменатель.
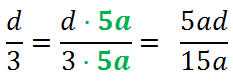
Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через «домики».
Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.
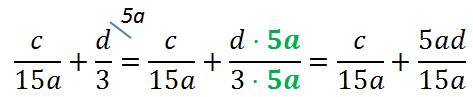
Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.
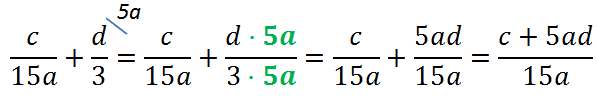
Рассмотрим пример вычитания дробей с разными знаменателями.
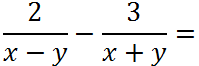
В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.
Рассмотрим знаменатели «(x − y)» и «(x + y)» обеих дробей и найдем для них общий знаменатель.
- Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
- Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.
Важно! 
Многочлены необходимо рассматривать целиком! Для удобства заключайте целый многочлен в скобки.
У нас есть два различных многочлена в знаменателях «(x − y)» и «(x + y)». Их произведение будет общим знаменателем, т.е. «(x − y)(x + y)» — общий знаменатель. 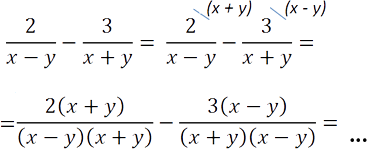
Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.
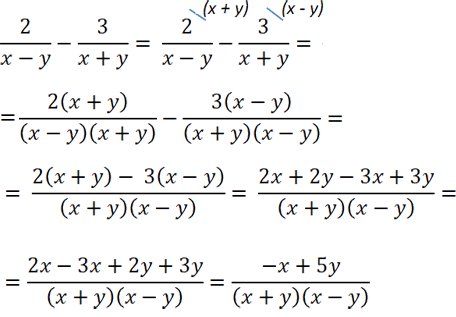
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|