
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Разложение функции в ряд Фурье
Разложение функции в ряд Фурье
Рассмотрим ряд вида
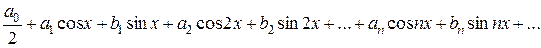
Числа 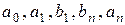 - называют коэффициентами тригонометрического ряда или его можно записать в виде
- называют коэффициентами тригонометрического ряда или его можно записать в виде 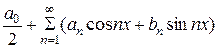
Допустим, что функция f (x) разлагается в тригонометрический ряд 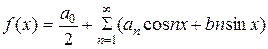
Если периодическая функция f(x) с периодом 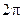 является суммой равномерно сходящегося на
является суммой равномерно сходящегося на 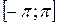 тригонометрического ряда (49), то коэффициенты этого ряда определяются по формулам:
тригонометрического ряда (49), то коэффициенты этого ряда определяются по формулам:
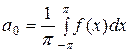 ,
, 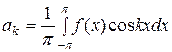 ,
, 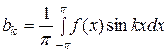 .
.
Данные коэффициенты называют коэффициентами Фурье, а тригонометрический ряд 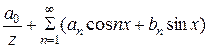 , коэффициенты которого определяются по формулам Фурье, называю рядом Фурье.
, коэффициенты которого определяются по формулам Фурье, называю рядом Фурье.
Ряды Фурье для чётных и нечётных функций.
Если f (x) – чётная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
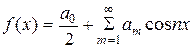 , где
, где 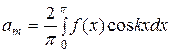 .
.
Если требуется разложить в ряд Фурье нечетную функцию, 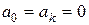 ,
, 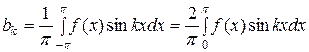 .
.
Ряд Фурье для нечетной функции имеет вид: 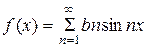 .
.
Если функция f (x) – задана на 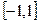 , где l – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряд Фурье:
, где l – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряд Фурье:
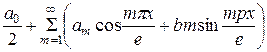 ,
,
где 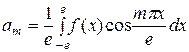 ,
, 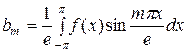 .
.
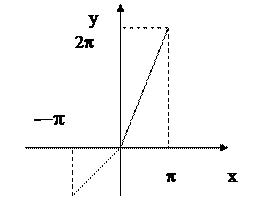
Пример 12. Разложить в ряд Фурье функцию f(x) = 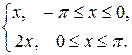 определенную в интервале (- p; p ).
определенную в интервале (- p; p ).
Решение. Вычислим коэффициенты Фурье функции f(x).
 а 0 =
а 0 = 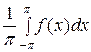 =
= 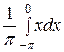 +
+ 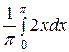 =
=
= 
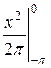 +
+ 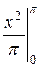 = -
= -  + p =
+ p =  .
.
а n = 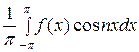 =
= 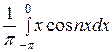 +
+
+ 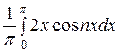 =
= 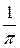 (I1 + I2). Интегралы I1, I2 интегрируем по частям: I1 =
(I1 + I2). Интегралы I1, I2 интегрируем по частям: I1 = 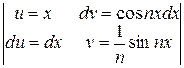 =
= 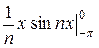 -
-
- 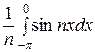 =
= 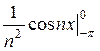 =
= 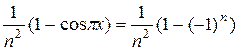 .
.
I2 = 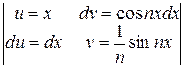 =
= 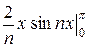 -
- 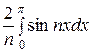 =
= 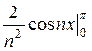 =
=
= 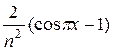 =
= 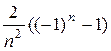 . Итак, аn =
. Итак, аn = 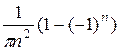 +
+ 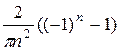 =
=
= 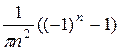 . Аналогично вычисляем коэффициент bn:
. Аналогично вычисляем коэффициент bn:
bn = 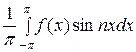 =
= 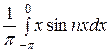 +
+ 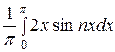 =
=
= 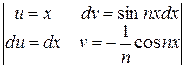 =
= 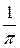 (
( 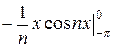 +
+ 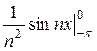 ) +
) +
+ 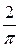 (
( 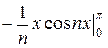 +
+ 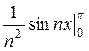 ) =
) = 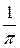 (-
(- 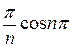 -
- 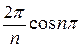 )=
)= 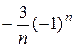 .
.
Следовательно, ряд Фурье для функции f(x) имеет вид:
f(x) = 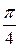 +
+ 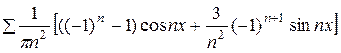 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|