
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема:. Тригонометрические ряды Фурье
Тема:. Тригонометрические ряды Фурье
Тригонометрический ряд.
Разложение функций в степенные ряды, т.е. разложения сложных функций на простые степенные функции вида 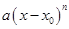 , не всегда возможны и не всегда удобны в приложениях.
, не всегда возможны и не всегда удобны в приложениях.
При изучении сложных периодических процессов естественно возникает задача о представлении функций, описывающих эти процессы в виде суммы конечного или бесконечного числа простых периодических функций.
В качестве таких функций берутся функции вида 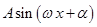 , или, что то же самое, функции вида
, или, что то же самое, функции вида 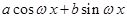 .
.
Если 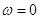 , то функция является постоянной, а если
, то функция является постоянной, а если 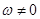 , то она является периодической с периодом
, то она является периодической с периодом 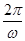 . В частности, каждая простая гармоника с
. В частности, каждая простая гармоника с 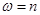 , где
, где 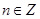 , имеет
, имеет 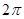 в качестве одного из своих периодов.
в качестве одного из своих периодов.
Рассмотрим задачу о разложении 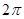 -периодической функции
-периодической функции 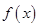 в ряд вида:
в ряд вида:
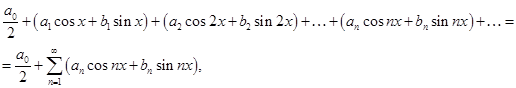
где 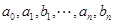 -- некоторые числа.
-- некоторые числа.
Такие ряды называются тригонометрическими, а числа 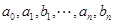 их коэффициентами.
их коэффициентами.
Член 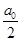 называется свободным членом (в виде
называется свободным членом (в виде 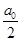 он берется для удобства).
он берется для удобства).
Определение. Тригонометрическим рядом Фурье для функции 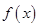 на отрезке
на отрезке 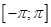 называется ряд вида
называется ряд вида 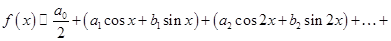
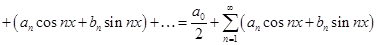 ,
,
коэффициенты которого, называемые коэффициентами Фурье для функции 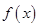 , вычисляются по следующим формулам:
, вычисляются по следующим формулам:
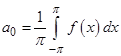 ;
;
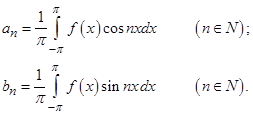
Условия, которые достаточно наложить на функцию 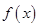 для того, чтобы её ряд Фурье сходился во всём промежутке разложения, определяются теоремой Дирихле:
для того, чтобы её ряд Фурье сходился во всём промежутке разложения, определяются теоремой Дирихле:
Если функция 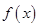 , заданная на отрезке
, заданная на отрезке 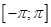 , удовлетворяет в этом промежутке условиям Дирихле, т.е.
, удовлетворяет в этом промежутке условиям Дирихле, т.е.
1) непрерывна за исключением только конечного числа точек разрыва I рода;
2) имеет конечное число экстремумов,
то ряд Фурье этой функции сходится на всём отрезке 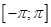 и сумма этого ряда:
и сумма этого ряда:
равна 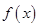 во всех точках непрерывности данной функции, лежащих внутри промежутка
во всех точках непрерывности данной функции, лежащих внутри промежутка 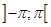 :
: 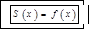 ;
;
равна 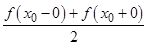 во всех точках разрыва:
во всех точках разрыва: 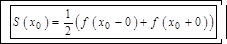 ;
;
равна 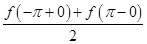 на концах промежутка:
на концах промежутка: 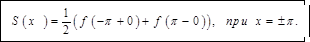
Так как члены ряда – функции периодические с периодом 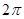 , то из сходимости ряда на отрезке
, то из сходимости ряда на отрезке 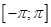 вытекает его сходимость на всей числовой оси, причем сумма этого ряда является периодической функцией с тем же периодом
вытекает его сходимость на всей числовой оси, причем сумма этого ряда является периодической функцией с тем же периодом 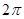 .
.
Тогда для того, чтобы ряд Фурье функции 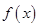 сходился именно к этой функции на всей числовой оси, надо и её считать периодической с периодом
сходился именно к этой функции на всей числовой оси, надо и её считать периодической с периодом 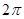 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|