Контакты

Случайная статья

Урок №39. Произведение синусов и косинусов.

Стр 1 из 2Следующая ⇒

Урок №39. Произведение синусов и косинусов.

Глоссарий по теме

Формулапроизведения синуса и косинуса:

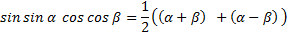
Формулапроизведения косинусов:

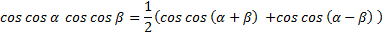
Формулапроизведения синусов:

Теоретический материал для самостоятельного изучения

Мы знаем, что для решения задач формулы используются как слева направо, так и справа налево.

Учитывая этот факт, выведем формулу произведения синуса и косинуса. По формуле синуса суммы и разности получаем:

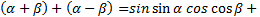
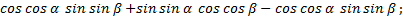
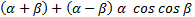
Значит, 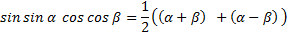(1)

По формуле косинуса суммы и разности получаем:

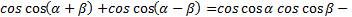
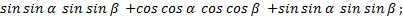
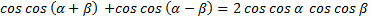, применив формулу справа налево, получим

формулу произведения косинусов:

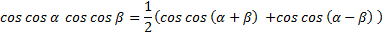(2)

Так же поступим с формулой разности косинусов:

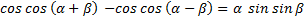
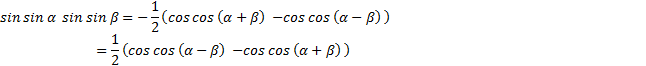
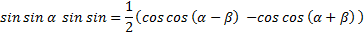(3)

Вывели формулу произведения синусов.

С помощью формул (1), (2), (3) можно произведение синусов и косинусов преобразовывать в сумму.

Пример.Преобразовать в произведение выражения:

а) ;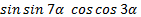

б) ;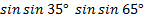

в) .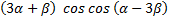

а) используем формулу (1) и получим:

;

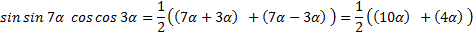б) используем формулу (3) и получим:

,

учитывая, что 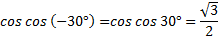, а по формуле приведения , наше выражение примет вид: ;

в) используем формулу (2) и получаем:

,

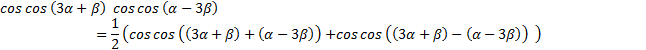Раскрываем скобки косинуса, упрощаем и получаем выражение, записанное в виде суммы

.

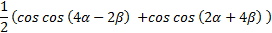Пример.Известно, что 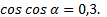Найти .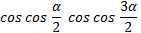

По формуле (2) получаем: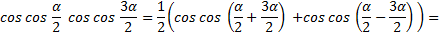

.

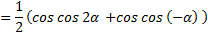Учитывая, что 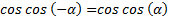и применяя формулу двойного аргумента

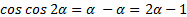, подставим 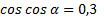, находим 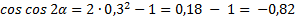. Подставим найденные значения в выражение:

.

12 Следующая ⇒

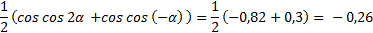© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.