Метод решения несобственного интеграла с бесконечным верхним (нижним) пределом

Несобственные интегралы
ПММ, 1 курс, 9 группа, Шебуняева Снежана

Несобственные интегралы первого рода. По сути, это тот же определённый интеграл, но в случаях, когда интегралы имеют бесконечный верхний или нижний пределы интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода. По сути, это тот же определённый интеграл, но в случаях, когда интеграл берётся от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не имеет, обращаясь в бесконечность.

Определенный интеграл 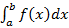называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:

· Предел a или b (или оба предела) являются бесконечными;

· Функция f(x) имеет одну или несколько точек разрыва внутри интервала [a,b].

Для сравнения.При введении понятия определённого интеграла предполагалось, что функция f(x) непрерывна на отрезке [a, b], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

***

Использование предела интеграла вместо самого несобственного интеграла.
Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода.

***

Итак, запись несобственного интеграла как 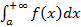отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f(x) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт,
т.е.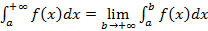

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся, и ему не приписывается никакого значения.

Метод решения несобственного интеграла с бесконечным верхним (нижним) пределом

Нужно найти первообразную (неопределенный интеграл), использовать предел при вычислении интеграла. Необходимо устремить верхний (нижний) предел интегрирования
к +∞ (-∞): b→+∞ (a→-∞).

Из вышесказанного следует формула для вычисления такого несобственного интеграла: 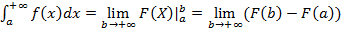или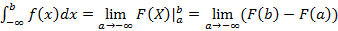

***

Несобственный интеграл с двумя бесконечными пределами интегрирования, обозначаемый символом 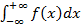, нужно предварительно представить в виде суммы двух несобственных интегралов, один из которых с конечным верхним пределом интегрирования, другой – с конечным нижним пределом интегрирования. Этот несобственный интеграл считается сходящимся, если оба предела существуют, когда a и b независимо друг от друга неограниченно возрастают по абсолютной величине.

12 Следующая ⇒