
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Геометрический смысл несобственного интеграла 1 рода
Геометрический смысл несобственного интеграла 1 рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Несобственные интегралы 2 рода
Пусть ƒ(x) определена на (a, b], терпит бесконечный разрыв в точке х=а и
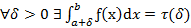 , тогда:
, тогда:
1. Если 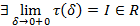 , то используется обозначение
, то используется обозначение 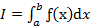 и интеграл называется несобственным интегралом Римана 2 рода. В этом случае называется сходящимся
и интеграл называется несобственным интегралом Римана 2 рода. В этом случае называется сходящимся
2. Если 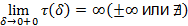 , то обозначение сохраняется, а
, то обозначение сохраняется, а 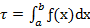 называется расходящимся к «∞», «±∞», или просто расходящимся
называется расходящимся к «∞», «±∞», или просто расходящимся
Пусть ƒ(x) определена на [a, b), терпит бесконечный разрыв при х=b и 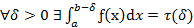 , тогда:
, тогда:
1. 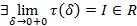 , то используется обозначение
, то используется обозначение 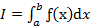 и интеграл называется несобственным интегралом Римана 2 рода. В этом случае называется сходящимся
и интеграл называется несобственным интегралом Римана 2 рода. В этом случае называется сходящимся
2. Если 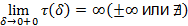 , то обозначение сохраняется, а
, то обозначение сохраняется, а 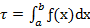 называется расходящимся к «∞», «±∞», или просто расходящимся
называется расходящимся к «∞», «±∞», или просто расходящимся
Если функция ƒ(x) терпит разрыв во внутренней точке с отрезка [a; b], то несобственный интеграл второго рода определяется формулой:
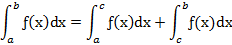
Геометрический смысл несобственного интеграла 1 рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.
Критерий Коши
1. Пусть ƒ(x) определена на множестве от [a, +∞) и 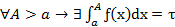 . Тогдa
. Тогдa
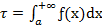 сходится
сходится 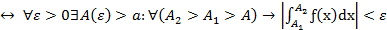
2. Пусть ƒ(x) определена на множестве от (a, b] и 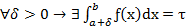 . Тогдa
. Тогдa
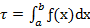 сходится
сходится 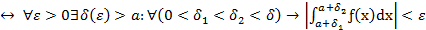
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|