
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только температура и давление, равно числу независимых компонентов системы минус число фаз плюс два.. Однокомпонентные системы
число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только температура и давление, равно числу независимых компонентов системы минус число фаз плюс два.
f = К – Ф +2
В общем случае, если число внешних факторов (помимо давления и температуры), одинаковых во всех фазах системы, равно п, правило фаз имеет вид
f = К – Ф + п
Если какой-либо внешний фактор, характеризующий систему, поддерживается постоянным, то число переменных становится на единицу меньше. Так, при p = const (или Т = const) правило фаз записывается следующим образом:
fусл. = К – Ф + 1
Однокомпонентные системы
Однокомпонентными системами являются такие системы, в которых отдельные фазы представлены одним и тем же веществом. Согласно правилу фаз Гиббса, число фаз в равновесной однокомпонентной системе равно:
Ф = 1 + 2 – f = 3 – f.
Наибольшее число степеней свободы для однокомпонентной системы существует при наименьшем числе фаз, которое в то же время не может быть менее единицы. Тогда
fmax = K + 2 – Ф = 1 + 2 – 1 = 2.
Основными параметрами такой системы являются температура и давление. Наименьшее число степеней свободы должно равняться нулю (отрицательным по определению оно быть не может). Тогда число фаз в однокомпонентной системе будет наибольшим:
Фmax = 1 + 2 – 0 = 3
Следовательно, ни одно индивидуальное вещество не может образовать равновесную систему, состоящую более чем из трех фаз. Так, невозможно подобрать такие значения Р и Т, при которых кремнезем (SiO2) существовал бы одновременно, например, в виде α-кварца, β-кварца, α-тридимита и α-кристобалита, находящихся в равновесии.
Для графического изображения состояния системы при различных значениях T, P и V используют систему координат из трех взаимно перпендикулярных осей, каждая из которых отвечает значениям одной переменной. Любое состояние однокомпонентной системы, отвечающее той или иной совокупности величин T, P, V, изображается в такой системе координат одной точкой. Совокупность экспериментально полученных точек дает диаграмму, состоящую из нескольких более или менее сложных поверхностей, расположенных определенным образом в пространстве. Точки, не лежащие на этих поверхностях, не имеют физического смысла. Справедливость последнего вполне очевидна, ибо каждому сочетанию Т и P соответствует единственно возможное значение V для данной фазы. Подобные диаграммы называются объемными (или полными) диаграммами состояния.
Однако полными диаграммами состояния обычно не пользуются, так как они громоздки и неудобны в обращении, а их изготовление весьма трудоемко. Всех этих недостатков лишены проекции таких диаграмм на одну из плоскостей, проходящих через оси координат. Наиболее употребительными параметрами, определяющими условия существования системы, являются Т и Р, так как они хорошо поддаются измерению и регулированию. Откладывая значения этих двух переменных по двум осям прямоугольной системы координат, строят двумерную (плоскую) диаграмму, которая приведена на рис. 1. Этот рисунок представляет собой проекцию полной диаграммы на плоскость Р–Т. Следует подчеркнуть, что на рис. 1 представлен вариант диаграммы простейшей однокомпонентной системы, которая характеризуется отсутствием полиморфных превращений и где понятие фазы совпадает с понятием агрегатного состояния.
Каждая точка на плоскости диаграммы выражает условия, при которых находится система, т.е. она представляет сочетание определенных величин температуры и давления. Благодаря этому вся диаграмма может быть разделена на несколько областей, каждая из которых охватывает всевозможные сочетания Т и Р, отвечающие равновесному существованию определенной фазы. Так, на рис. 1 область Г отвечает условиям равновесного существования газообразной фазы, область Ж – жидкой фазы и область Тв – твердой фазы. Точки, отражающие состояние и условия существования системы, называются фигуративными точками.
В соответствии с правилом фаз число степеней свободы однофазной однокомпонентной системы будет равно:
f = К + 2 – Ф = 1 + 2 – 1 = 2.
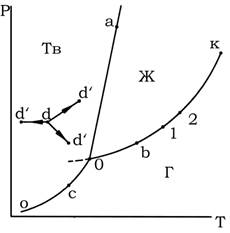
Рис. 1. Диаграмма состояния однокомпонентной системы в координатах давление — температура
Пограничные линии ОК, Оа (Оа’), Оо принадлежат обеим соприкасающимся областям, и каждая точка на этих линиях может отвечать как совместному существованию двух фаз, так и наличию только одной из них. Следует иметь в виду, что всякий фазовый переход при постоянных Т и Р сопровождается изменением энтальпии системы, вследствие чего, например, в точке а жидкость и кристаллы сосуществуют лишь в том случае, если энтальпия системы выше энтальпии твердого состояния, но ниже энтальпии жидкого состояния, т. е. когда фазовый переход еще не завершен. Если переход еще не начался или уже завершен, то система представляет собой одну фазу. Следовательно, кривая Оа (Оа’)отвечает равновесному сосуществованию твердой и жидкой фаз; кривая Оо – твердой и газообразной фаз; кривая ОК – жидкой и газообразной фаз.
Двухфазная однокомпонентная система является моновариантной:
f = K + 2 – Ф = 1 + 2 – 2 = 1.
Следовательно, если изменить условия существования системы, сохраняя равновесие между двумя фазами, например, жидкостью и паром (точка b на рис. 5.1), то можно произвольно изменить лишь один параметр состояния, например температуру. Давление же при этом следует изменить на вполне определенную величину так, чтобы фигуративная точка системы b смещалась строго по кривой ОК (точка 1 или 2).
Точка О отвечает равновесному сосуществованию трех фаз при данных температуре и давлении. Эту точку называют тройной. Любое изменение температуры или давления выводит фигуративную точку из положения О, и она попадает в области, где возможно равновесное сосуществование либо двух фаз, либо одной фазы. Равновесное сосуществование трех фаз возможно лишь при строго определенном сочетании значений температуры и давления. Для такого состояния число степеней свободы равно нулю, система инвариантна (нонвариантна):
f = K + 2 – Ф = 1 + 2 – 3 = 0.
Кривая испарения заканчивается точкой К, которая называется критической точкой и где исчезает всякое различие между жидкостью и паром. В этой точке на систему наложено дополнительное ограничение – тождественность свойств жидкости и пара, поэтому система в критической точке также инвариантна.
Кривые испарения, плавления, сублимации определяются уравнением Клапейрона–Клаузиуса
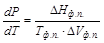
Упрощённые уравнения Клапейрона–Клаузиуса для плавления:
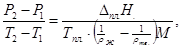
где Δпл.Н – мольная теплота плавления, Т пл. – температура плавления; Т1 и Т2 – температуры плавления при давлениях Р1 и Р2 соответственно, М молекулярный вес, а ρж. и ρтв. плотности жидкой и твердой фазы.
Для сублимации и испарения:
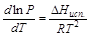
Зная зависимость давления насыщенного пара от температуры можно аналитически и графически найти теплоту испарения, сублимации и даже теплоту плавления в тройной точке. Для этого можно воспользоваться теми же формулами, что и при определении теплового эффекта эндотермической реакции по изобаре Вант-Гоффа.αβ
Например, если эмпирическое уравнение имеет вид:
lnP=A+B/T +ClnT +DT+ET-2 , то
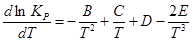 ,
,
а 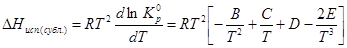


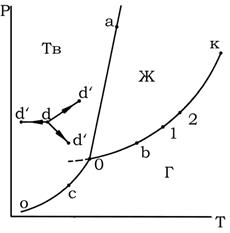
Рис.2
Графически теплоту испарения и теплоту сублимации можно определить по формулам:
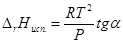
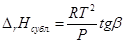
По закону Гесса теплота сублимации в тройной точке равна сумме теплот испарения и плавления. Откуда можно найти теплоту плавления. Подобно данному методу можно определить теплоту плавления из графика lnP от 1/Т
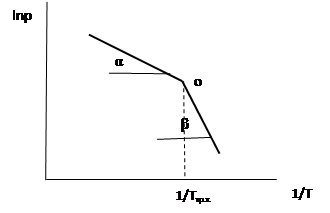 |
ΔH пл.= ΔH субл.- ΔH исп.=R(tgβ-tgα)
Существуют также простые эмпирические формулы для расчета теплот фазовых переходов.Наиболе часто используются следующие:
а) Уравнение Трутона
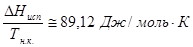
б) Теплота плавления органических веществ 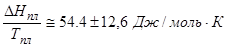 .
.
Зная зависимость давления насыщенного пара от температуры можно рассчитать, как было показано выше температуры плавления, кипения и сублимации. Отсюда можно найти изменение внутренней энергии.
Для плавления:
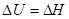
Для сублимации и возгонки:
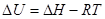
Т.к. рассматриваются только равновесные фазовые переходы, при постоянных Р и Т 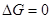 . А следовательно
. А следовательно 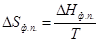 . Из этого положения можно также вычислить
. Из этого положения можно также вычислить
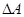 фазового перехода,
фазового перехода,
а) при плавлении, 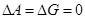
б) при испарении:
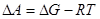
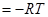
Вопросы и задачи:
1. Нарисуйте фазовую диаграмму воды.
2. Рассчитайте вариантность системы в различных точках.
3. Теплота плавления и плотность жидкой и твердой ртути при температуре тройной точки (234,3К) равны соответственно 11,8Дж/г,13,69, 14,19 г/см3. Вычислить на какую величину изменится давление, чтобы температура плавления стала235,3К.
4. Вычислить температуру плавления, давление насыщенного пара и теплоту плавления серебра в тройной точке, если: для твердого серебра lgp=13,892-14020/T, для жидкого серебра lgp=13,347-13340/T
5. Вычислить теплоту плавления хлора, если уравнение зависимости давления насыщенного пара в Па от температуры имеет вид: Р=3,58‧106-3,37‧104Т+80,11Т2.
6. Зависимость давления насыщенного пара от температуры: lgp=34,5-2406/T-9,26lgT+0,0037T. Получить температурную зависимость изменения энтальпии, энергии Гиббса, энтропии теплоемкостей
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|