Разложение вектора по трем некомпланарным векторам. Решение задач.

Стр 1 из 3Следующая ⇒

Разложение вектора по трем некомпланарным векторам. Решение задач.

Определение:

Вектором называется направленный отрезок. У вектора 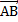точка А – начало вектора, точка В – конец.

Для вектора важна не только длина, но и направление.

Определение:

Коллинеарными называют векторы, принадлежащие одной и той же или параллельным прямым.

Коллинеарные векторы могут быть сонаправленными и противонаправленными.

Определение:

Равными называют коллинеарные сонаправленные векторы, длины которых равны.

Любой вектор можно единственным образом отложить от произвольной точки.

Для сложения векторов применяются правила треугольника, параллелограмма, многоугольника и параллелепипеда.

При умножении вектора на положительное число его длина умножается на это число, а направление остается неизменным. При умножении вектора на отрицательное число его длина умножается на это число, а направление меняется на противоположное.

Новым для векторов в пространстве относительно векторов на плоскости является понятие компланарности.

Определение:

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Разложение вектора на плоскости и в пространстве

Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам (рис. 1, 2):

Рис. 1. Векторы на плоскости

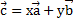
Рис. 2. Разложение вектора через два неколлинеарных

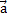Данный факт легко доказывается. Пусть . Из точки С проводим прямую CB, параллельно вектору . Получаем вектор , коллинеарный вектору 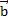. Аналогично из точки С проводим прямую CА, параллельно вектору 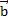. Получаем вектор 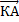, коллинеарный вектору 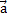. Это означает, что существуют такие два числа х и у, причем единственные, что:

Если вектор 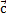можно представить в виде 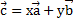, где х и у – конкретные числа, то векторы и 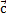компланарны.

Если заданы три некомпланарных вектора, то мы можем однозначно разложить любой заданный четвертый вектор через три заданных. Например, заданы некомпланарные векторы и 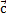. Тогда любой вектор можно представить в виде суммы: , где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.

12 3 Следующая ⇒