
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дискретная и непрерывная случайные величины
2.2. Дискретная и непрерывная случайные величины
Если значения, которые может принимать данная случайная величина 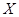 , образует дискретный (конечный или бесконечный) ряд чисел
, образует дискретный (конечный или бесконечный) ряд чисел 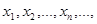 то и сама случайная величина
то и сама случайная величина 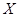 называется дискретной.
называется дискретной.
Если же значения, которые может принимать данная случайная величина 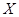 , заполняют конечный или бесконечный промежуток (а, в) числовой оси Ох, то случайная величина называется непрерывной.
, заполняют конечный или бесконечный промежуток (а, в) числовой оси Ох, то случайная величина называется непрерывной.
Каждому значению случайной величины дискретного типа 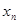 отвечает определенная вероятность
отвечает определенная вероятность 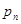 ; каждому промежутку (а, в) из области значений случайной величины непрерывного типа также отвечает определенная вероятность
; каждому промежутку (а, в) из области значений случайной величины непрерывного типа также отвечает определенная вероятность 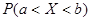 того, что значение, принятое случайной величиной, попадает в этот промежуток.
того, что значение, принятое случайной величиной, попадает в этот промежуток.
2.3. Закон распределения случайной величины
Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Закон распределения дискретной случайной величины обычно задается рядом распределения:
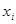
| 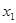
| 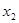
| 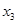
| … | 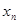
|
 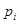
| 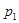
| 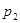
| 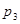
|  … …
| 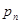
|
При этом 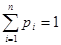 , где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины
, где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины 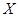 .
.
Закон распределения непрерывной случайной величины удобно задавать с помощью функции плотности вероятности 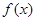 .
.
Вероятность 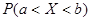 того, что значение, принятое случайной величиной
того, что значение, принятое случайной величиной 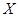 , попадет в промежуток (а, в), определяется равенством
, попадет в промежуток (а, в), определяется равенством
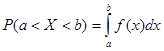 .
.
График функции 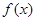 называется кривой распределения. Геометрически вероятность попадания случайной величины в промежуток (а, в) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х=а, х=в.
называется кривой распределения. Геометрически вероятность попадания случайной величины в промежуток (а, в) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х=а, х=в.

Задача 1. Даны вероятности значений случайной величины 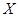 : значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины
: значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Построить ряд распределения случайной величины 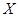 .
.
Решение. Расположив значения случайной величины в возрастающем порядке, получим ряд распределения:
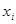
| ||||
 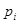
| 0,4 | 0,2 | 0,1 | 0,3 |
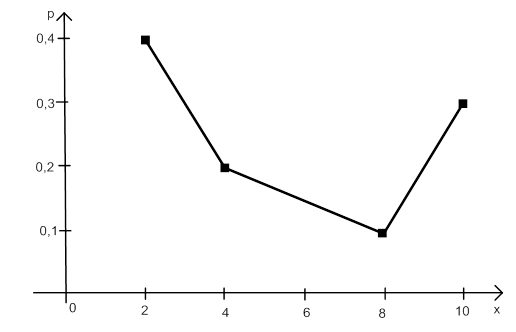
Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8; 0,1) и (10; 0,3). Соединив последовательные точки прямолинейными отрезками, получим многоугольник (или полигон) распределения случайной величины 
|
Задача 2.Разыгрываются две вещи стоимостью по 5000 руб и одна вещь стоимостью 30000 руб. Составить закон распределения выигрышей для человека, купившего один билет из 50.
Решение: (самостоятельно)
Закон распределения случайной величины имеет вид:
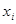
| |||
 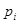
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|