Тема: Событие. Вероятность случайного события.

Тема: Событие. Вероятность случайного события.

Повторение. Решить

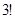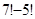Пример 1. Вычислить: а) ; б) ; в) .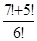

Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?

Пример 3. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?

Пример 4. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

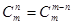
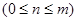
(по определению полагают и );

Пример 5. Найти 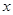, если известно, что . ( оформить в тетради)

Решение.

Так как 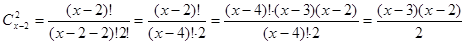, то получим

, .

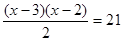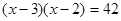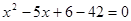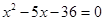
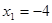По определению сочетания следует, что 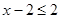, 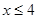. Т.о. .

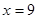Ответ: 9

2. (Конспект. ) Понятие о случайном событии. Виды событий. Вероятность события

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

достали пронумерованный шар (А);

достали шар с четным номером (В);

достали шар с нечетным номером (С);

достали шар без номера (Д).

Какие из них образуют полную группу?

Решение. А - достоверное событие; Д - невозможное событие;

В и С - противоположные события.

Полную группу событий составляют А и Д, В и С.

Вероятность события, рассматривается как мера объективной возможности появления случайного события.

3. Классическое определение вероятности

Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим

.

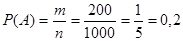Задача 2. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.

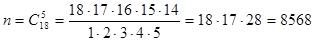
Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:

.

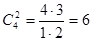
Число способов выборки трех качественных деталей из 14 имеющихся качественных равно

.

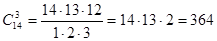Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет

.

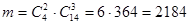Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:

.

12 3 Следующая ⇒