ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Линии на плоскости и их уравнения.

Пусть на плоскости задана декартова система координат и некоторая линия L.

Определение. Уравнение Ф(х, у) = 0 называется уравнением линии L, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии L, и не удовлетворяют координаты ни одной точки, не лежащей на линии L.

Пример. (х – х_o)² + (y – y_o)² = R² - уравнение окружности радиуса R с центром в точке (х_o, y_o).

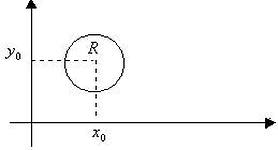
Замечание. Часто удобно использовать параметрические уравнения линии:

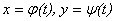где функци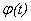и и 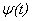непрерывны по параметру t.

Примеры.

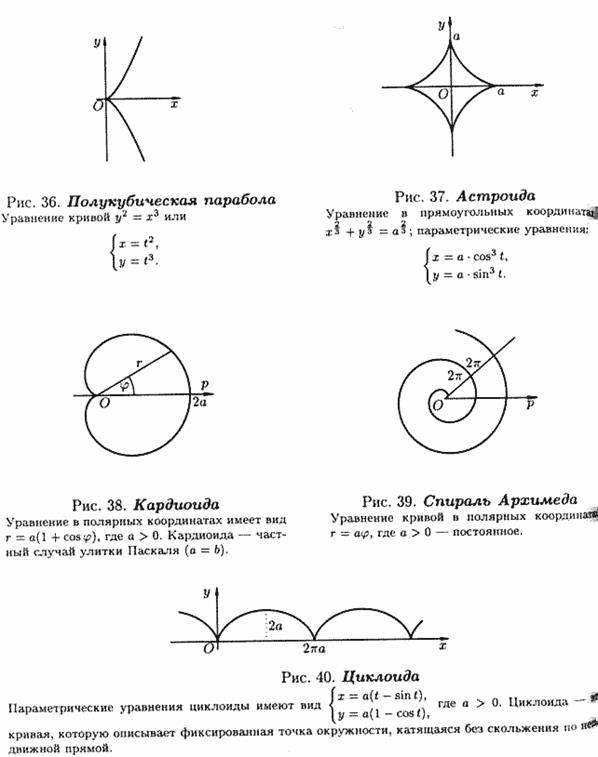
Прямая на плоскости. Различные формы уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.

Рассмотрим различные виды уравнений прямой на плоскости.

Пусть прямая проходит через точку М₀ (x₀, y₀) перпендикулярно вектору n = {A, B}. Тогда вектор 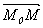, где М(х, у) – произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению

А(х – х₀) + В(у – у₀) = 0 - (7. 3)

уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Замечание. Вектор n называется нормалью к прямой.

Преобразуем уравнение (7. 3) к виду:

Ах + Ву + (-Ах₀ – Ву₀) = 0.

Обозначив -Ах₀ – Ву₀ = С, получим общее уравнение прямой:

Ах + Ву + С = 0. (7. 4)

Получим теперь уравнение прямой, проходящей через точку М₀ (x₀, y₀) параллельно вектору q = {l, m}. Так как вектор 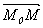, где М(х, у) – произвольная точка прямой, коллинеарен q, координаты любой точки данной прямой удовлетворяют уравнению

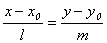, (7. 5)

называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М₁(х₁, у₁) и М₂(х₂, у₂), ее направляющим вектором можно считать 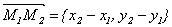, и из уравнения (7. 5) следует:

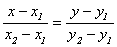- (7. 6)

уравнение прямой, проходящей через две заданные точки.

Пример.

Составим уравнение прямой, проходящей через точки М(1, 2) и N(5, -3). Уравнение (7. 6) примет вид:

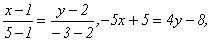
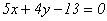- общее уравнение данной прямой.

Обозначив за t значения равных дробей, стоящих в левой и правой частях уравнения (7. 5),

можно преобразовать это уравнение к виду:

x = x₀ + lt, y = y₀ + mt - (7. 7)

параметрические уравнения прямой.

Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k – тангенс угла, образованного прямой и осью Ох, и записать уравнение прямой в виде:

у = kx + b - (7. 8)

уравнение прямой с угловым коэффициентом.

Действительно, все точки прямой l₁, параллельной l и проходящей

через начало координат, удовлетворяют уравнению у = kх, а

ординаты соответствующих точек на прямой l отличаются от них

на постоянную величину b.