Хелпикс

Главная

Контакты

Случайная статья



Тема 3 Множественная регрессия и корреляция



Тема 3 Множественная регрессия и корреляция

3. 1 Изучаемые вопросы

Линейная модель множественной регрессии. Классический метод наименьших квадратов для модели множественнойрегрессии. Множественное линейное уравнение регрессии. Показатели теснотысвязи, частной и множественной корреляции. Обычный и скорректированныйпоказатели множественной детерминации. Проверка гипотез о значимостичастного и множественного коэффициентов корреляции, регрессионныхкоэффициентов и уравнения множественной регрессии в целом. Понятиемультиколлинеарность.

3. 2 Практическое занятие 7, 8, 9. Множественная регрессия и корреляция

Исходные данные.

Фактическое конечное потребление домашних хозяйств (в текущих ценах) на душу населения, тыс. руб. (У); средний размер назначенных пенсий тыс. руб. (Х1); величина прожиточного минимума (в среднем на душу населения) (Х2)тыс. руб. (таблица 1).

Таблица 1 - Исходные данные для модели

 
У 

106, 84

132, 54

165, 92

175, 36

195, 74

245, 52

277, 98

306, 97

329, 28

343, 19
Х2

2, 73

3, 12

4, 20

5, 19

7, 48

8, 20

9, 04

9, 92

10, 79

11, 99
Х3

3, 42

3, 85

4, 59

5, 15

5, 69

6, 37

6, 51

7, 31

8, 05

9, 70

 

Задание:

1. Заполнить таблицу 2.

 


Таблица 2 – Данные для построения модели

t Y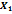
                             
                             
                             
                             
                             
                             
                             
                             
                             
                             
∑                              
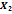
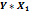
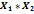
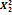
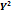
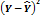
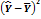
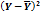
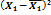
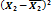
Среднее значение                              

2. Рассчитать показатели корреляции в таблице 3.

Таблица 3 -  Расчет коэффициентов корреляции

Формула Результат расчета
   
 
 

 

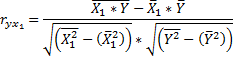
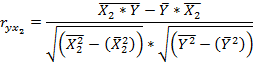
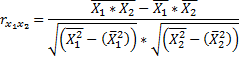
3. Построить матрицу в таблице 4.

Таблица  4 - Матрица коэффициентов

  Y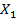
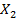
 Y    
   
   

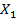
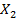
Интерпретация:

0, 1- 0, 3- слабая связь

0, 3-0, 5 – умеренная связь

0, 5-0, 7- заметная связь

0, 7-0, 9- тесная связь

0, 9-0, 99- весьма тесная
4. Определитьпараметры а, b1 и b2 уравнения множественной линейной регрессии по системе уравнений:

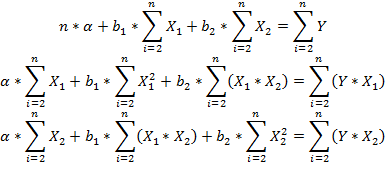
Получим систему уравнений:

 

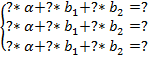
5. Переписать систему уравнений в матричном виде и решить его методом Гаусса.

6. Найти параметры уравнения:

-?

 -?

 -?

 

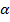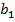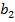7. Составить уравнение в виде:

 

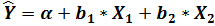
8. Дать количественную оценку частным коэффициентам эластичности:

 ?

?

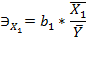
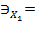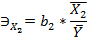
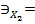9. Определить расчетное значение критерия Фишера (таблица 5).

 

Таблица 5 – Сравнение табличного и фактического значениякритерия Фишера

Формула Результат расчета
 
 
 
 

 

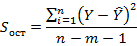
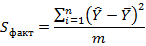
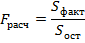
10. Рассчитать совокупный коэффициент множественной корреляции:

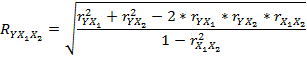
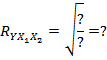
11. Провести оценку статистической значимости коэффициентов регрессии b1 и b2 по t-критерию (таблица 6).

Таблица 6 - Оценка статистической значимости коэффициентов регрессии

Формула Результат расчета
 
 
 
 
 

 

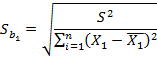
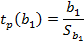
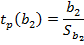
12. Сформулировать выводы по каждому пункту заданий
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.