Билеты для экзамена по курсу “Элементы математической логики” (2-ой курс)

Билеты для экзамена по курсу “Элементы математической логики” (2-ой курс)

Билет №1.

1. Понятие множества. Элементы множества.

Множество — это совокупность определённых объектов рассматриваемых как единое целое.

Элементы множества — это объекты из которых состоит множество.

2. Определить истинность двухместного предиката D (х, y) = “остаток х/y = 0”:

     ∀ x∀ yD(x, y) = 0 («для любого x и y выполняется условие двухместного предиката
(остаток х/y = 0) — ЛОЖЬ »)
     Ǝ xƎ yD(x, y) = 1 («найдется x и y для которых выполняется условие двухместного предиката
(остаток х/y = 0) — ИСТИНА »)
     ∀ xƎ yD(x, y) = 1 («для любого x найдется y для которого выполняется условие двухместного предиката (остаток х/y = 0) — ИСТИНА »)

Доп. инфо:

Билет №2.

1. Способы задания множеств. Подмножества.

Способы задания множеств:

- перечислением его элементов (только для конечных множеств) —
T = {1, 2, 3, 4};

- с помощью характеристического условия (предиката) P(x) — T = {x | P(x)} «множество всех элементов x, для которых высказывание P(x) истинно» (описательный, состоит в том, что указывается характерное свойство, которым обладают все элементы множеств);

- с помощью порождающей процедуры (она описывает, как получить элементы множества) — T ={x | x∈ Z ∧ x²< 10}

Множество A называют подмножеством множества B, если все элементы множества A являются также элементами множества B. Обозначение: A⊂ B.

2. Найти простые импликанты для функции f(x, y)=x🡪 y

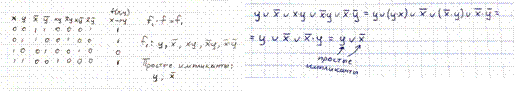Доп. инфо:

Импликанта → некая формула f₁ — импликанта формулы f, если f₁ — элементарное произведение и f₁* f= f₁

Простая импликанта → импликанта f1 формулы f называется простой, если после отбрасывания любой литеры из f1 не получается формула, являющаяся импликантой формулы f.

Элементарное произведение — конъюнкт, в который любая переменная входит не более 1 раза (сама или её отрицание).

Билет №3.

1. Изображение множеств. Диаграмма Эйлера-Венна.

Множества можно схематично изображать диаграммами (кругами) Эйлера–Венна. Диаграмма Эйлера – Венна состоит из прямоугольника, иллюстрирующего универсальное множество, и замкнутых линий (обычно кругов), все точки внутри которых изображают элементы некоторого множества А

2. Алфавит логики предикатов.

Алфавит:

1. Символы предметных переменных → обычно строчные латинские буквы ± индексы;

2. Символы предикатов → обычно прописные латинские буквы ± индексы;

3. Логические символы → , &, ∨, →, ⇔;

4. Символы кванторов → ∀, ∃.

5. Скобки и запятые.

Билет №4.

1. Сравнение множеств. Декартово произведение множеств.

Множество A называется подмножеством множества B, если все элементы A содержатся в B (A ⊂ B или B ⊃ A).

Множества A и B называются равными, если они совпадают, т. е. любой элемент, который есть в A, есть и в B, и наобором (т. е. они состоят из одних и тех же элементов) (A = B, если ∀ a, b [a ∈ A → a ∈ B and b ∈ B → b ∈ A]).

Декартово произведение — множество всевозможных упорядоченных пар.
X x Y = {(x, y) | x ∈ X, y ∈ Y} (если x! = y, то (x, y)! = (y, x))

n(X) = m (кол-во элементов в множестве X)

n(Y) = k (кол-во элементов в множестве Y)

n(X x Y) = mk (кол-во элементов в декартовом произведении множеств X и Y)

n(X₁ x X₂ x … x X_n) = n(X₁) * n(X₂) * … * n(X_n)

Доп. инфо:

Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.

Если множества А и В не имеют общих элементов, т. е. нет элементов, принадлежащих одновременно А и В, то говорят, что эти множества не пересекаются.

2. Логические связки для образования сложных высказываний в алгебре предикатов.

Логические связки: (не - отрицание), & (и - конъюнкция),
∨ (или - дизъюнкция), → (если то - импликация), ⇔ (если и только если - эквивалентность), ⊕ (либо…, либо… - неравнозначность / исключающее ИЛИ / сложение по модулю 2).

Билет №5.

1. Мощность и степень множества. Числовые множества.

Мощность множества — кол-во элементов этого множества.

Степень множества равна числу подмножеств данного множества. (2ⁿ)

Числовые множества:

1. N — натуральные числа;

2. Z — целые числа;

3. Q — рациональные числа;

4. I — иррациональные числа;

5. R — действительные числа;

6. C — комплексные числа.

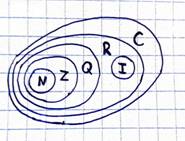2. Определение формулы в логике предикатов.

Формула:

1. Пропозициональные переменные (простые высказывания) — формулы;

2. Если A, B — формулы, то A, A& B, A∨ B, A→ B — формулы;

3. Формулами являются только выражения построенные в соответствии с пунктами 1 и 2.

Билет №6.

1. Основные операции над множествами. Свойства операций.

Основные операции:

1. Пересечение множеств A и B — A ∩ B = {x | x ∈ A и x ∈ B}

2. Объединение множеств A и B — A ∪ B = {x | x ∈ A или x ∈ B}

3. Разность множеств A и B — A \ B = {x | x ∈ A и x ∉ B}

4. Симметричная разность множеств A и B — A Δ B = {x | (x ∈ A) & (x ∉ В ) ∨
(x ∉ A) & (x ∈ B)}

Свойства операций:

1. Идемпотентность — A ∩ A = A, A ∪ A = A;

2. Коммутативность — A ∩ B = B ∩ A, A ∪ B = B ∪ A;

3. Ассоциативность — (A ∩ B) ∩ C = A ∩ (B ∩ C), (A ∪ B) ∪ C = A ∪ (B ∪ C);

4. Дистрибутивность — A ∩ (B ∪ C) = A ∩ B ∪ A ∩ C, A ∪ (B ∩ C) =
(A ∪ B) ∩ (A ∪ C);

5. Принцип двойственности (закон де Моргана) - (A ∩ B) = A ∪ B, (A ∪ B) = A ∩ B

2. Дан одноместный предикат Q(x) = x²< 1, x ϵ R. Определить Q(-3) -?, Q(1) -?

Q(-3) = Л

Q(1) = Л

Решение для Q(-3):

подставим -3 в одноместный предикат (Q(x) = x²< 1, x ϵ R) и получим (-3)²< 1, 9 < 1, что является ЛОЖЬЮ.

Билет №7.

1. Формула включений и исключений.

n(A) = кол-во элементов в множестве A.

n(A ∪ B) = n(A) + n(B) — n(A ∩ B)

n(A ∪ B ∪ C) = n(A ∪ (B ∪ C)) = n(A) + n(B ∪ C) — n(A ∩ (B ∪ C)) =

= n(A) + n(B) + n(C) — n(A ∩ B) — n(A ∩ C) — n(B ∩ C) + n(A ∩ B ∩ C)

2. Определить истинность трехместного предиката B(x, y, z) = x² +y²< z, x, y, z ϵ R; B(1, 1, -2) -?, B(1, 1, 2) -?

B(1, 1, -2) = Л

B(1, 1, 2) = Л

Билет №8.

1. Соответствие между множествами. Отображение. Область определения. Область значений.

Соответствием между элементами множества Х и элементами множества Y называется любое подмножество декартова произведения этих множеств.

Отображение множества A во множество B — это правило, по которому каждому элементу множества A ставится в соответствие элементы множества B (в том случае, если в соответствие ставится единственный элемент, данное правило называется однозначно определённой функцией (или просто функцией)).

Область определения — D(f) - (x) - множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Область значения — E(f) — (y) - множество, состоящее из всех значений, которые принимает функция.

2. Дать определение высказывания, n-местного предиката.

Предикатом местности n (n-местным предикатом), определенным на предметной области X, называют отображение множества X во множество высказываний.

Обозначение: P(х1, х2, . . . , хn) - n-местный предикат, определенный на X={х1, х2, . . . , хn}.

Дадим другие определение предиката.

– Предикатом местности n (n-местным предикатом), определенным на предметной области M, называют логическую функцию принимающую истину или ложь. (написано в тетради)

Билет №9.

1. Бинарные отношения, их свойства и типы.

Бинарные отношения между элементами множеств A и B — любое подмножество декартово произведения A на B (R ⊂ A x B)

Св-ва бинарных отношений:

1. Рефлексивность (∀ x ∈ M(xRx)); «для любого x в множестве M существует пара (x, x)»

2. Антирефлексивность (∀ x ∈ M (xRx)); «для любого x в множестве M не существует пара (x, x)»

3. Корефлексивность (∀ x, y ∈ M(xRy → x = y)); «для любого x, y если в множестве M есть пара (x, y), то x равен y»

4. Симметричность (∀ x, y ∈ M(xRy → yRx)); «для любого x, y если в множестве M есть пара (x, y), то в множестве M также существует пара (y, x)»

5. Антисимметричность (∀ x, y ∈ M(xRy ∩ yRx → x = y)); «для любого x, y если в множестве M есть пара (x, y) и (y, x), то x равен y»

6. Асимметричность (∀ x, y ∈ M(xRy → (yRx))). «для любого x, y если в множестве M есть пара (x, y), то в множестве M не существует пары (y, x)»

7. Транзитивность (∀ x, y, z ∈ M(xRy ∩ yRz → xRz)); «для любого x, y, z если в множестве M есть пара (x, y) и (y, z), то в множестве M существует пара (x, z)»

8. Связность (∀ x, y ∈ M(x ≠ y → xRy ∪ yRx)). «для любого x, y если x! = y, то в множестве M есть пара (x, y) или (y, x)»

Типы бинарных отношений:

1. ① и ⑦ поражают отношение квазипорядка;

2. ①, ④ и ⑦ поражают отношение эквивалентности;

3. ①, ⑤ и ⑦ поражают отношение (частичного) порядка;

4. ②, ⑤ и ⑦ поражают отношение строгого порядка;

5. ⑤ и ⑦ поражают отношение линейного порядка.

2. Привести к нормальной форме (ДНФ или КНФ) f(x, y, z)= x*y* (x*y*z)*(y ∨ z).

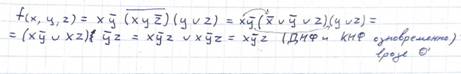Билет №10.

1. Простые и составные высказывания. Суждения. (у меня в лекции это нет: ( )

Суждение – форма мышления, в которой что-либо утверждается или отрицается.

Высказывание – это повествовательное предложение, о котором можно сказать истинно оно или ложно.

Простые высказывания — высказывание, которое не может быть разбито на более простые высказывания (про него можно всегда однозначно сказать, что оно истинно или ложно, не интересуясь его структурой).

Сложные (составные) высказывания — высказывания, построенные из простых высказываний при помощи так называемых логический связок ( (не), & (и),
∨ (или), → (если то), ⇔ (если и только если).

2. Определить множество А: А={x ϵ R | x² – 3x – 10 > 0}. A -?

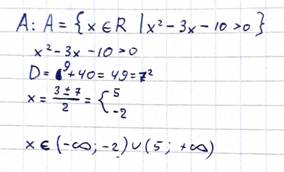(не уверена как записать ответ)

Билет №11.

1. Булевы функции. Равенство функций.

Булева функция (функция алгебры логики, логическая функция) — функция от n переменныхx₀, x₁, …, x_n, в которой аргументы и сама функция принимает значения 0 или 1.

Функции равны (эквивалентны), если на всяком наборе нулей и единиц значения функций совпадают.

_x0

2. Определить множество А: А={x ϵ R | (x-9) / (x +3) > 0}. A -? (здесь тоже)

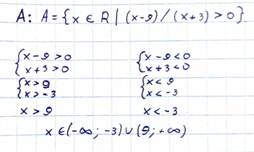Билет №12.

1. Задание булевых функций посредством элементарных операций. (неуверенна, что здесь имеется ввиду)

Если в логическую функцию вместо переменных подставить некоторые булевые функции, то в результате получается новая булевая функция. (Пусть задана элементарная булева функция x ∪ y. Подставим вместо x функцию x1↓ x2. Получаем функцию трех переменных (x1↓ x2)vy. Если вместо переменной y подставить, например, x3⊕ x4, то получаем новую функцию от четырех переменных: (x1↓ x2)v(x3⊕ x4). )

2. Даны множества: А={ 1, 2…20 }, B = { 10, 11…40 }, А, В Ϲ N. A ٨ B -?

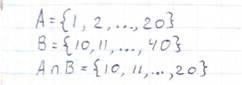Билет №13.

1. Таблицы истинности. Эквивалентные функции.

Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных

значениях её аргументов.

Функции равны (эквивалентны), если на всяком наборе нулей и единиц значения функций совпадают.

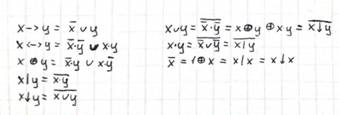2. Даны множества А, В, С. n(A) = 42, n(B) = 30, n(C) = 28, n(A B) = 5, n(A C) = 10, n(B C) = 8,
n(A B C) = 3; n(A U B U C) -?

n(A ∪ B ∪ C) = n(A) + n(B) + n(C) — n(A ∩ B) — n(A ∩ C) — n(B ∩ C) + n(A ∩ B ∩ C)

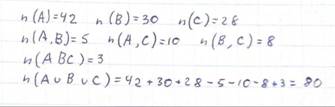Билет №14.

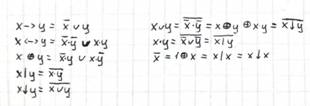1. Основные эквивалентности. Законы логики.

Законы логики:

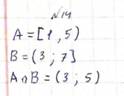
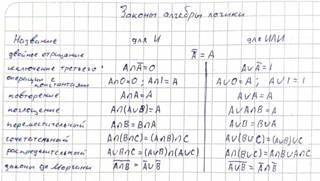2. Даны множества: А = [1, 5), B = (3, 7], A, B Ϲ R; A Ʌ B -?

Билет №15.

1. Функциональная полнота. Теорема Поста. Базисы.

Функциональная полнота множества логических операций или булевых функций — это возможность выразить все возможные значения таблиц истинности с помощью формул из элементов этого множества.

Теорема Поста (критерий полноты): Система F булевых функций является полной тогда и только тогда, когда она включает хотя бы одну функцию не сохраняющую константу 0, не сохраняющую константу 1, не само двойственную, не линейную, не монотонную.

Базисы:

1. S₁ = {, &, ∨ }

2. S₂ = {, & }

3. S₃ = {, ∨ }

4. S₄ = {1, &, ⊕ }

5. S₅ = {|}

6. S₆ = {↓ }

7. S₇ = {→, 0}

2. Даны множества: А={ x | x ϵ N, x > =9 }, B = { x | x ϵ N, x < 15 }; А ∩ В -?

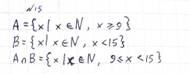Билет №16.

1. Минимизация булевых функций.

Для минимизации булевых функций используется метод Квайна — способ представления функции в ДНФ или КНФ с минимальным набором переменных.

2. Даны множества: А={ x | x ϵ N, x ≥ 3² }, B = { x | x ϵ N, x < 30 } А ∩ В -?

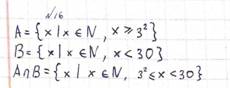Билет №17.

1. Нормальные формы. Совершенные нормальные формы.

Формула в булевой логике может быть записана в дизъюнктивной (ДНФ) и в конъюнктивной (КНФ) нормальной форме.

ДНФ - нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов (AB ∨ AB (Сумма произведений)).

КНФ - нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов ((A ∨ B) ∧ (A ∨ B) (Произведение логических сумм)).

Совершенные нормальные формы → если в каждом члене нормальной формы представлены все переменные, причем в каждом отдельном конъюнкте или дизъюнкте любая переменная входит ровно 1 раз (либо сама, либо ее отрицание), то эта форма называется совершенной нормальной формной.

2. f(x, y, z)=10010100. Построить СДНФ.

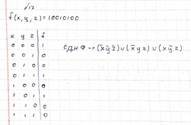Билет №18.

1. Алгоритм построения нормальных форм.

1. С помощью законов алгебры логики заменить все имеющиеся в формуле операции основными: конъюнкцией, дизъюнкцией, отрицанием.

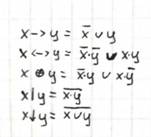2. Применить, где это возможно законы де Моргана.

(x∩ y) = x∪ y

(x∪ y) = x∩ y

3. Избавиться от знаков двойного отрицания.
x = x
4. Применить, если нужно, формулы поглощения.
x ∪ (x ∩ y) = x
x ∩ (x ∪ y) = x

2. Дать определение n-местного предиката.

Обозначение: P(х1, х2, . . . , хn) - n-местный предикат, определенный на X={х1, х2, . . . , хn}.

Дадим другие определение предиката.

– n-местный предикат - это связное повествовательное предложение, содержащее n переменных и обладающее следующим свойством: при фиксации всех переменных о нем (предложении) можно сказать, истинно оно или ложно.
or
– Предикатом местности n (n-местным предикатом), определенным на предметной области M, называют логическую функцию принимающую истину или ложь. (написано в тетради)

Билет №19.

1. Минимизация ДНФ методом Квайна. (скорей всего спросит про то, что проходили на паре (то что на фото))

Метод Квайна относится к числу таких методов минимизации функций алгебры логики, которые позволяют представлять функции в ДНФ и КНФ с минимальным числом членов и минимальным числом букв в членах.

Получение сокращенной формы. Пусть заданная функция f представлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: Операции склеивания и операции поглощения. Для выполнения операции склеивания выявляются в выражении пары членов вида a ∩ x и a ∩ x. Затем проводится склеивание таких пар членов: a ∩ x∪ a ∩ x= a ∩ (x ∪ x) = a,
Далее проводится операция поглощения. Она основана на равенстве a ∪ a ∩ x = a ∩ (1 ∪ x) = a. Операции склеивания и поглощения проводятся последовательно до тех пор, пока их выполнение оказывается возможным. Полученное выражение представляет собой сокращенную форму логического выражения заданной функции, а члены его - простые импликанты функции.

2. Даны множества: А={ 6х+2 | x ϵ Z }, B = { 6x | x ϵ Z }, C = { 6x+4 | x ϵ Z };
А U В U C -?

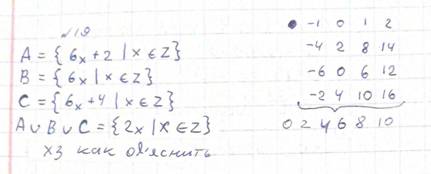Билет №20.

1. Алгебра Жигалкина в базисе S4.

Множество булевых функций, заданных в базисе Жигалкина (базисе S4) - {1, &, ⊕ } - называется алгеброй Жигалкина.

Основные св-ва:

1. Коммутативность: x ⊕ y = y ⊕ x; x & y = y & x

2. Ассоциативность: x ⊕ (y ⊕ z) = (x ⊕ y) ⊕ z; x & (y & z) = (x & y) & z

3. Дистрибутивность: x & (y ⊕ z) = (x & y) ⊕ (x & z)

4. Св-во констант: x & 1 = x; x & 0 = 0; x ⊕ 0 = x

5. x ⊕ x = 0; x & x = x

2. Даны множества: А={ 9х+7 | x ϵ Z }, B = { 9x+4 | x ϵ Z }, C = { 9x+1 | x ϵ Z };
А U В U C -?

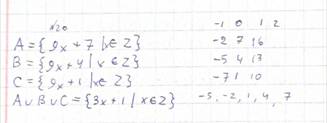Билет №21.

1. Канонический полином Жегалкина. Теорема Жегалкина.

Канонический полином Жегалкина:

Полином Жегалкина представляет собой сумму по модулю два попарно различных произведений неинвертированных переменных, где ни в одном произведении ни одна переменная не встречается больше одного раза, а также (если необходимо) константы 1[1]. Формально полином Жегалкина можно представить в виде:

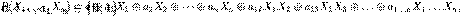Теорема Жегалкина:

- Каждая булева функция представляется в виде полинома Жегалкина единственным образом.

2. Даны множества: А={ 3x | x ϵ Z }, B = { 6x | x ϵ N}; А\ В -?

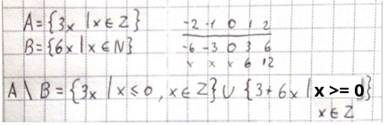Билет №22.

1. Методы построения полинома Жегалкина.

Методы построения полинома Жегалкина:
1. Метод неопределённых коэффициентов.

2. Приведение формулы к виду {, & }, затем замена x = 1 ⊕ x, раскрываем скобки (св-во 3 (дистрибутивность - (x & (y ⨁ z) = (x & y) ⨁ (x & z)))) и применяем св-ва 4 (св-во констант - (x & 1 = x; x & 0 = 0; x ⨁ 0 = x)) и 5 (x ⊕ x = 0; x & x = x).

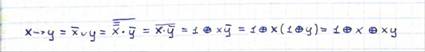2. Построить таблицу истинности для функции: f(x, y) = x ↔ y v x.

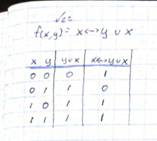
Билет №23.

1. Понятие предиката. Примеры.

Предикат — то, что высказывается в суждении об объекте (наличие или отсутствие того или иного признака в объекте)

— отображение произвольных множеств на множества высказываний.

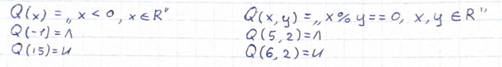2. Построить таблицу истинности для функции: f(x, y) = x | y v y.

Билет №24.

1. Тождественно истинные и тождественно ложные предикаты.

1. тождественно истинный предикат - при любой подстановке вместо переменных x₁, x₂, …, x_n любых конкретных предметов a₁, a₂, …, a_n из множеств M₁, M₂, …, M_n соответственно он превращается в истинное высказывание;

- на любом наборе аргументов он принимает истинное значение

2. тождественно ложный предикат - при любой подстановке вместо переменных x₁, x₂, …, x_n любых конкретных предметов a₁, a₂, …, a_n из множеств M₁, M₂, …, M_nсоответственно он превращается в ложное высказывание;

- на любом наборе аргументов он принимает ложное значение

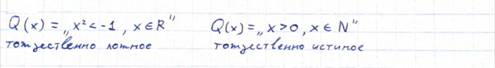2. Исследовать эквивалентность функций: f1(x, y) = x ٨ y v (x ٨ y v x ٨ y), f2(x, y) =
((x ٨ y) + x) + y.

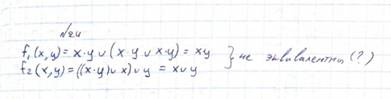Билет №25.

1. Кванторы.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката
Квантор всеобщности (∀ x) – выражение «для всех » («для любого »);

Квантор существования (∃ x) – выражение «существует такое, что... ».

2. Записать в базисе S1 = { , ^, v } функцию f(x, y, z) = x ↔ ( y + z )

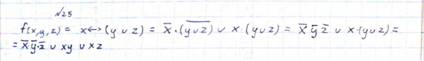Билет №26.

1. Правила вывода исчисления предикатов. (мы это вроде не записывали, хз что это)

1. Пусть (A(x) → B) и B не содаржит переменной x, тогда: ((∃ x A(x) → B)

Это правило связывания квантором существования.

2. Пусть (B → A(x)) и B не содержит переменной x, тогда: (B → (∀ x A(x)))

Это правило связывания квантором общности.

3. Связанную переменную формулы B можно заменить другой переменной, не являющейся свободной в B.

Это правило связанной переменной.

2. Определить тип формы ( КНФ, ДНФ ): (x ∨ x ∨ y) ∧ (y ∨ z ∨ x) ∧ z

x ∧ y ∧ z

x ∧ y ∧ x ∧ x

Возможный ответ:

1. КНФ

2. КНФ и ДНФ

3. КНФ и ДНФ

Билет №27.

1. Математическая индукция. Полная математическая индукция.

Математическая индукция— метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n+1 — шаг индукции, или индукционный переход.

Полная индукция - это умозаключение, в котором общее заключение делается на базе изучения всех предметов или явлений данного класса (т. е. перебором всех элементов (? )).

2. Привести к нормальной форме ( КНФ, ДНФ ): x y (x y z)( y v z).

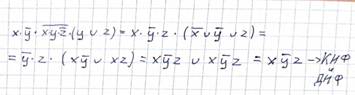(ДНФ — ((x∧ y∧ z) ∨ 0), КНФ - ((x∨ 0)∧ (y∨ 0)∧ (z∨ 0)))

Билет №28.

1. Определение алгоритма.

Алгоритм — точный набор инструкций для исполнителя, который (набор) приводит к решению задачи за конечное время.

— программа для универсального исполнителя.

Универсальный исполнитель — исполнитель, который может моделировать работу любого другого исполнителя. Т. е. для любого алгоритма, написанного для любого исполнителя, существует эквивалентный алгоритм для универсального исполнителя.

— некоторая модель вычислений, которая задаёт способ описания алгоритма и их выполнения.

2. Формулы де Моргана для предикатов со связанными переменными.

(∀ x P(x)) = ∃ x (P(x))

(∃ x P(x)) = ∀ x (P(x))

Билет №29.

1. Машина Тьюринга.

Машина Тьюринга — абстрактный исполнитель (абстрактная вычислительная машина), которыйбыл предложен Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Конструкция:

1. Бесконечная лента разделённая на ячейки (память);

2. Читающее и записывающее устройство, которое передвигается вдоль ленты;

3. Программируемый автомат.

Автомат управляет кареткой, посылая ей команды в соответствии с записанной в него программой. Лента выполняет роль памяти компьютера, автомат — роль процессора, а каретка служит для ввода/вывода данных

2. Алфавит логики предикатов.

Алфавит:

1. Символы предметных переменных → обычно строчные латинские буквы ± индексы;

2. Символы предикатов → обычно прописные латинские буквы ± индексы;

3. Логические символы → , &, ∨, →, ⇔;

4. Символы кванторов → ∀, ∃.

5. Скобки и запятые.