
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
49. Коэффициент Фехнера.
50. Коэффициент корреляции Пирсона
Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреляции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона.
В общем виде формула для подсчета коэффициента корреляции такова:
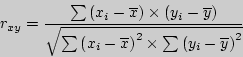
где - 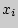 значения, принимаемые переменной X,
значения, принимаемые переменной X,
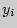 - значения, принимаемые переменой Y,
- значения, принимаемые переменой Y,
 - средняя по X,
- средняя по X,
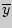 - средняя по Y.
- средняя по Y.
Расчет коэффициента корреляции Пирсона предполагает, что переменные 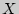 и
и 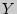 распределены нормально. Даная формула предполагает, что из каждого значения
распределены нормально. Даная формула предполагает, что из каждого значения 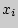 переменной X, должно вычитаться ее среднее значение
переменной X, должно вычитаться ее среднее значение  . Это не удобно, поэтому для расчета коэффициента корреляции используют не данную формулу, а ее аналог, получаемый с помощью преобразований:
. Это не удобно, поэтому для расчета коэффициента корреляции используют не данную формулу, а ее аналог, получаемый с помощью преобразований:
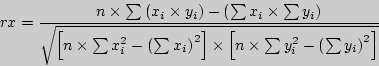
49. Коэффициент Фехнера.
К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Фехнером. Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков.
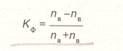 Если ввести обозначения: па - число совпадений знаков отклонений индивидуальных величин от средней, пв - число несовпадений знаков отклонений, то коэффициент Фехнера можно записать таким образом:
Если ввести обозначения: па - число совпадений знаков отклонений индивидуальных величин от средней, пв - число несовпадений знаков отклонений, то коэффициент Фехнера можно записать таким образом:
Коэффициент Фехнера может принимать различные значения в пределах от -1до +1. Если знаки всех отклонений совпадут, то пв = 0 и тогда показатель будет равен 1, что свидетельствует о возможном наличии прямой связи. Если же знаки всех отклонений будут разными, тогда па = 0 и коэффициент Фехнера будет, равен -1, что дает основание предположить наличие обратной связи.
48. Заработная плата – показатель, который входит составляющей при расчётах себестоимости, издержек производства. Основным показателем, характеризующим заработную плату, является средняя её величина как для отдельных групп работников, так и для предприятия в целом.
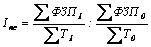
Динамика средней заработной платы анализируется с применением индексного метода, который может быть представлен следующей системой показателей:, где ФЗП1, ФЗП0 – фонды начисленной заработной платы отдельных категорий работников в отчётном и базисном периодах соответственно, Т1 Т0 – численность этих же категорий работников в отчётном и базисном периодах; 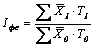 , где
, где 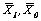 – средняя заработная плата по категориям персонала в отчётном и базисном периодах; .
– средняя заработная плата по категориям персонала в отчётном и базисном периодах; . 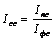 Кроме указанной системы индексов возможно применение индексного метода в оценке запланированных, фактических и т. д. показателей, характеризующих плановую, сверхплановую и фактическую экономию, причём анализировать можно как отдельные показатели по группам работников, так и по всему предприятию в целом:
Кроме указанной системы индексов возможно применение индексного метода в оценке запланированных, фактических и т. д. показателей, характеризующих плановую, сверхплановую и фактическую экономию, причём анализировать можно как отдельные показатели по группам работников, так и по всему предприятию в целом:
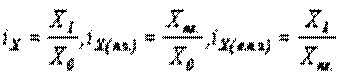
, каждый из указанных индивидуальных индексов характеризует отдельную категорию работников. Первый индекс показывает, как фактически изменилась заработная плата у одной из категорий работников в относительных показателях, а разность между числителем и знаменателем дроби представляет собой фактическое изменение в натуральных измерителях заработной платы этой категории. Второй индекс показывает запланированное изменение заработной платы, а третий – сверхплановое изменение. При анализе изменений фонда заработной платы (ФЗП) за счёт изменений заработной платы у отдельных категорий работников, следует рассматривать соответствующие индексы:
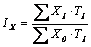
– фактическое изменение (фактическую экономию или перерасход) ФЗП за счёт изменения заработной платы у отдельных категорий работников (разность между числителем и знаменателем дроби показывает фактическое изменение ФЗП за счёт изменений заработной платы в натуральных измерителях);
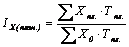 – плановое изменение (плановую экономию или перерасход) ФЗП;
– плановое изменение (плановую экономию или перерасход) ФЗП;
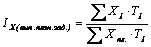 – сверхплановое изменение (сверхплановую экономию или перерасход) ФЗП.
– сверхплановое изменение (сверхплановую экономию или перерасход) ФЗП.
47. Степень распространения различных форм и систем оплаты труда характеризуется с помощью следующих статистических следующие показателей:
1) доля отработанного времени в рамках определенной формы или системы оплаты труда в общем количестве отработанного времени:
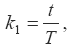
где t – отработанное время в рамках определенной формы или системы оплаты труда;
T – общее количество отработанного времени;
2) доля работников, получающих заработную плату по той или иной форме или системе отплаты труда в общей численности работников:
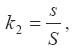
где s – количество работников, получающих заработную плату по определенной форме или системе оплаты труда;
S – общая численность работников;
3) доля заработной платы, начисленной по соответствующей форме или системе оплаты труда, в общем фонде заработной платы наемных работников:
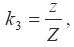
где z – заработная плата, начисленная по соответствующей форме или системе оплаты труда;
Z – общий фонд зарплаты.
46. Территориальные индексы представляют собой разновидность относительных величин сравнения, когда сопоставляются сложные показатели, относящиеся к одному и тому же периоду времени, но к разным территориям (городам, районам, областям, государствам). На основе территориальных индексов выполняются международные сопоставления.
Территориальный индекс товарооборота — это отношение суммы выручки от продажи в одном из районов к аналогичному показателю в другом. Один из районов (например, Б) берется за базу сравнения т. е.
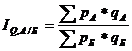
Различие объемов товарооборота вызвано различием ассортимента и количества проданных товаров, а также цен.
Территориальный индекс физического объема товарооборота рассчитывается по следующей формуле:
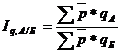
где р — средняя межрайонная цена товара каждого вида,
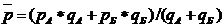
Территориальный индекс цен определяется:
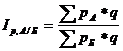
где q - суммарный по двум районам объем продаж каждого вида товара.
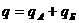
Такие сложные взвешивающие показатели применяются для того, чтобы результаты расчета были обратимыми, т. е. чтобы выполнялись соотношения:
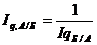 и
и 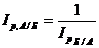
Условия индексной модели могут нарушаться, хотя и не очень существенно. Использование таких территориальных индексов для анализа абсолютной разницы товарооборотов дает в только приближенный результат.
Территориальные индексы можно также рассчитывать:
с использованием соизмерителей только района А или только района Б;
как среднюю геометрическую из двух территориальных индексов, рассчитанных с разными территориальными весами.
45. Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:
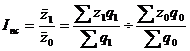
Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).
Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции: 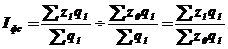
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|