
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 1.
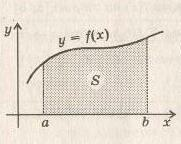
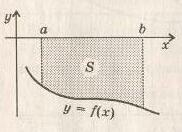
Площадь криволинейной трапеции
Определение: фигура, ограниченная графиком функции 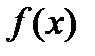 , прямыми
, прямыми 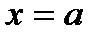 и
и 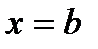 и осью абсцисс – называется криволинейной трапецией.
и осью абсцисс – называется криволинейной трапецией.
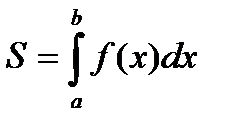
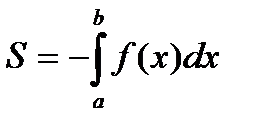
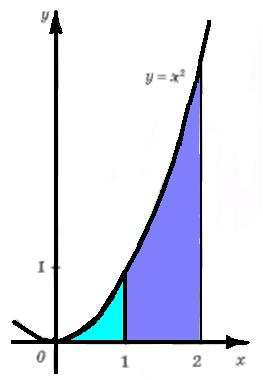
Пример 1.
Вычислим площадь S криволинейной трапеции, ограниченной графиком функции f(x)=x2, прямыми у=0, х=1 и х=2.
Для функции f(x)=x2 одной из первообразных является функция F(x)= 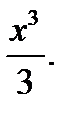 Следовательно,
Следовательно, 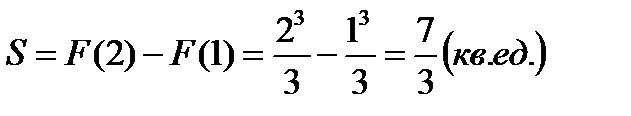
Пример 2.
Вычислить площадь криволинейной трапеции, ограниченной осью Ох, прямыми х=-1, х=2 и параболой у=9-х2.
Построим график функции у=9-х2 и изобразим данную трапецию
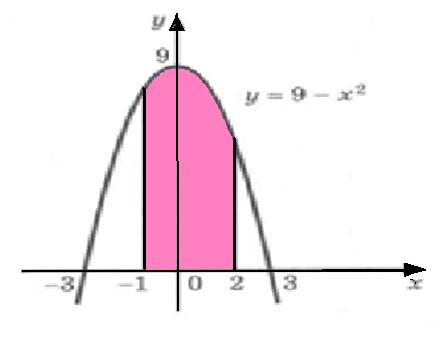
Искомая площадь S равна интегралу 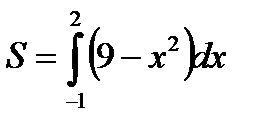 .
.
По формуле Ньютона - Лейбница находим
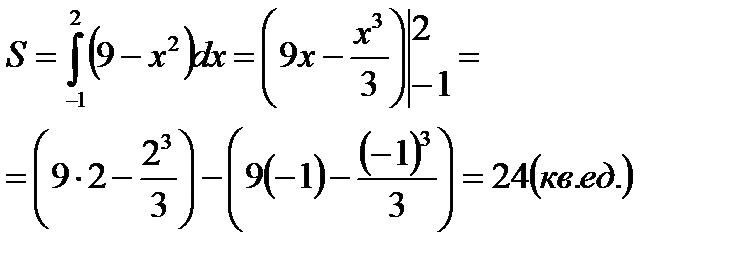
Пример 3.
Найдите площадь фигуры, ограниченной осью Ох, и параболами у=х2, у=2х-х2 . Построим графики функций у=х2, у=2х-х2и найдём абсциссы точек пересечения этих графиков из уравнения 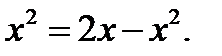
Корни этого уравнения 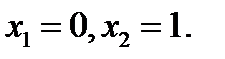
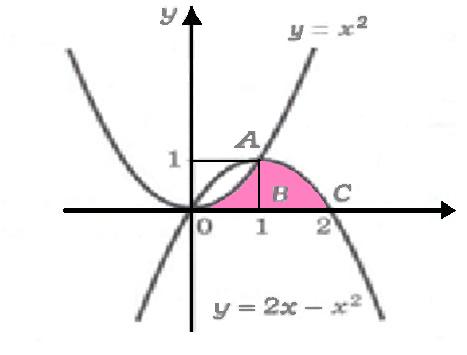
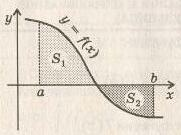
Из рисунка видно, что эта фигура состоит из двух криволинейных трапеций. Следовательно, искомая площадь равна сумме площадей этих трапеций.
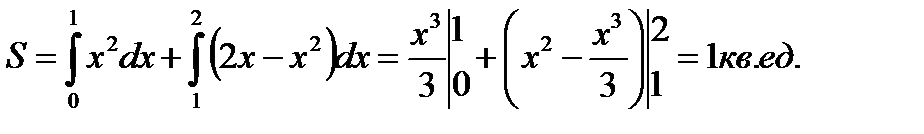
Пример 4.
Найдите площадь S фигуры, ограниченной отрезком 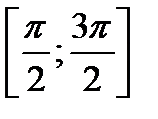 оси Ох и графиком функции
оси Ох и графиком функции 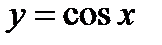 на этом отрезке.
на этом отрезке.
Заметим, что площадь данной фигуры равна площади фигуры, симметричной данной относительно оси Ох, т. е. площади фигуры, ограниченной отрезком 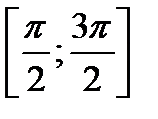 оси Ох и графиком функции
оси Ох и графиком функции
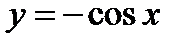 на отрезке
на отрезке 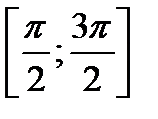 .
.
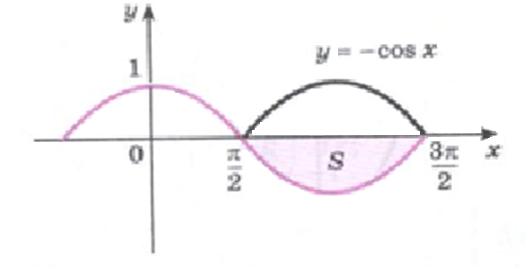
На этом отрезке 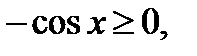 и поэтому
и поэтому 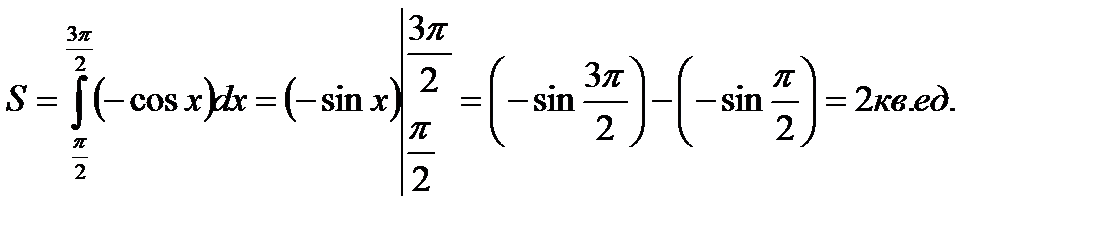
Пример 5.
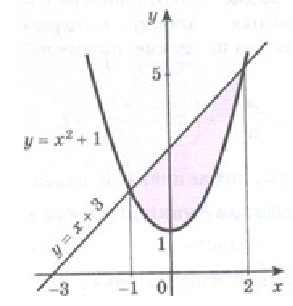
Найдите площадь S фигуры, ограниченной параболой у=х2 +1 и прямой у=х+3. Построим графики функций у=х2 +1 и у=х+3.
Найдём абсциссы точек пересечения этих графиков из уравнения
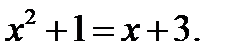 Это уравнение имеет корни
Это уравнение имеет корни 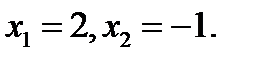
Из рисунка видно, что искомую площадь можно найти как разность площадей S1 и S2 двух трапеций, опирающихся на отрезок 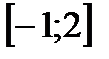 , первая из которых ограничена сверху отрезком прямой у=х+3, а вторая – дугой параболы у=х2 +1. Так как
, первая из которых ограничена сверху отрезком прямой у=х+3, а вторая – дугой параболы у=х2 +1. Так как
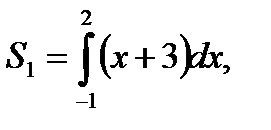
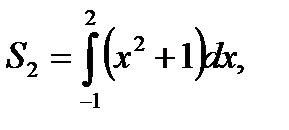 то
то
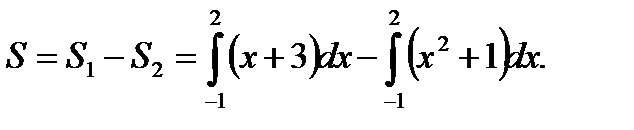
Используя свойство первообразных, можно записать S в виде одного интеграла:
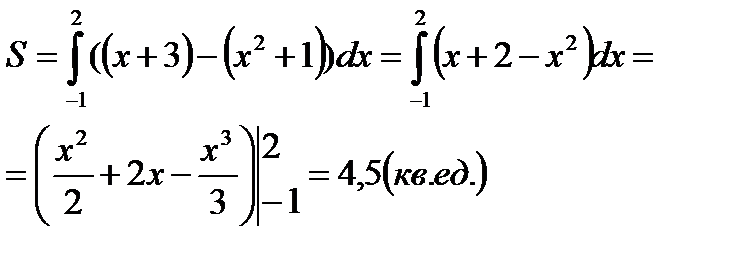
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|