Параллельность прямых и плоскостей

Параллельность прямых и плоскостей

	Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB. 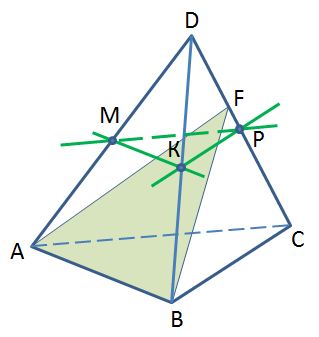1) МР 2) РК 3) МК 4) МК и РК
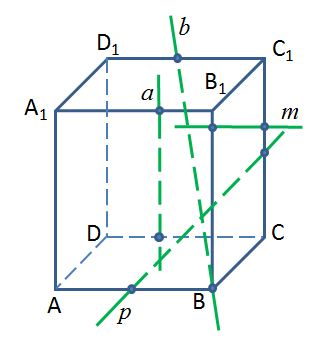	АВСDA₁B₁C₁D₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A₁AD? 1) а 2) b 3) p 4) m
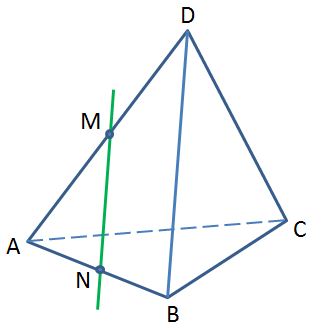	В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN? 1) DAB 2) DBC 3) DAC 4) ABC
	Выберите верные высказывания: 1) Параллельные прямые не имеют общих точек. 2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости. 3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей. 4) Существует параллелепипед, у которого все углы граней острые. Ответ: ______
	Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Назовите параллельные прямые. 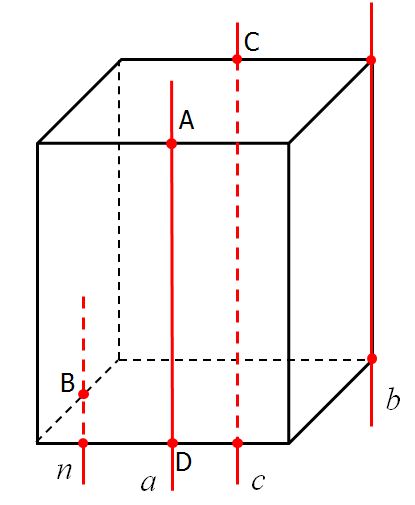1) a \|\| n 2) a \|\| b 3) b \|\| c 4) a \|\| c
	Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания: 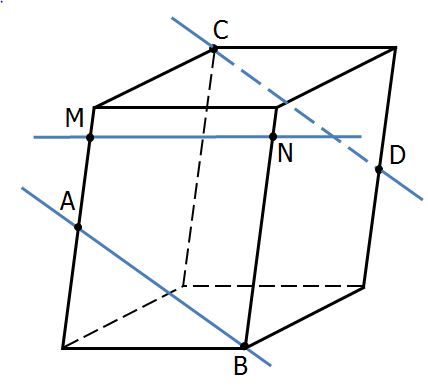1) Прямые СD и MN пересекаются. 2) Прямые АВ и MN скрещивающиеся 3) Прямые АВ и СD параллельные. 4) Прямые АВ и MN пересекаются Ответ: ______
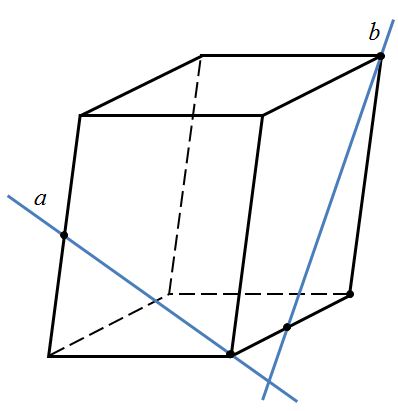	Определите взаимное расположение прямых. 1) a и b – пересекающиеся прямые 2) a и b – параллельные прямые 3) a и b – скрещивающиеся прямые
	Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых. 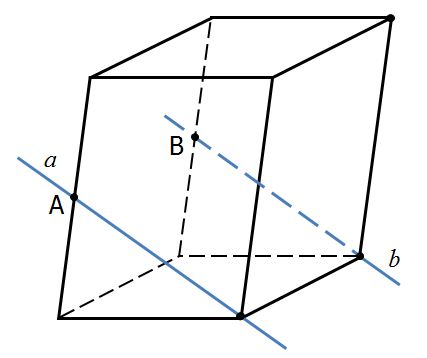1) a и b – пересекающиеся прямые 2) a и b – параллельные прямые 3) a и b – скрещивающиеся прямые
	Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD. 1) они параллельны 2) скрещиваются 3) пересекаются
	В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения. Ответ: ____