
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Бірнешеайнымалыфункцияэкстремумыныңқажеттішарты.
Интернет заттар жә не Big Data 1901 - группа студенті
Ержанов Рамазан
№1Ө ТС
1. Бірнешеайнымалыфункцияэкстремумының қ ажеттішарты.
2. Бірнешеайнымалыфункцияэкстремумының жеткіліктішарты.
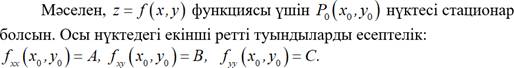
 |
3.
 |
Шарттыэкстремум.
Анық талмағ анеселіктерә дісі.

№2Ө ТС
Функцияның экстремумы
Аң ық тама.
Егер y=f(x) функциясы x0 нү ктенің белгілі бір δ аймағ ында: x0– δ < x < x0 + δ аң ық талса ә рі осы аймақ та f(x) > f(x0) (f(x) < f(x0))болса онда бұ л нү кте y=(x) функциясының минимум (максимум) нү ктесі деп аталады.
Функцияның максимум жә не минимум нү ктелерің функцияның экстремум нү ктелері деп атайды.
Мысалдар.
a). y=sinx функциясы x1= –900 нү ктеде минимумғ а ие, ал x2= 900 нү ктеде максимумғ а ие.
b). y= |1-x2| функциясы x1= 0 нү ктеде максимумғ а ие, ал минимум нү ктелері екеу x2= -1, x3= 1.
Теорема.
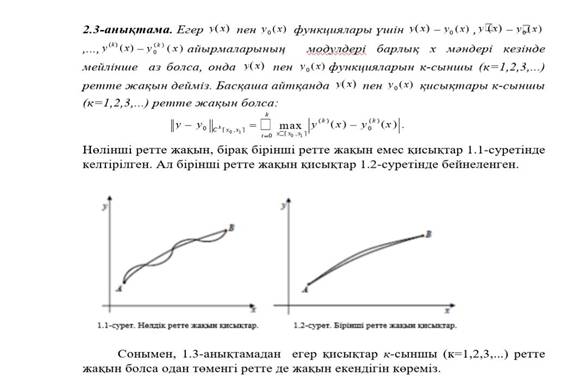
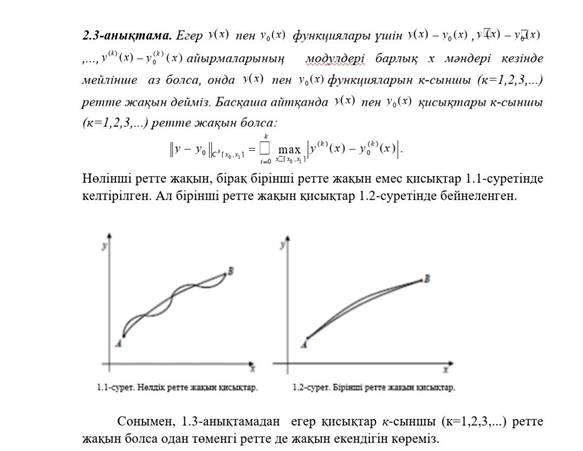
Егер (a; b) сегментінде дифференцияланданатың y=f(x) функциясы x0∈ (a; b) нү ктеде экстермумғ а ие болса, онда бұ л нү ктеде оның туындысы нө лге тең: f ′ (x0)=0

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|