Вопросы для подготовки к экзамену по дисциплине «Математика 1» для студентов

Вопросы для подготовки к экзамену по дисциплине «Математика 1» для студентов

3МТпб-01-11оп и 3ТТпб-01-11оп, второй семестр обучения,

2015-2016 учебный год

1. Сформулируйте правила действий над бесконечными числами. Определите понятие неопределенного выражения.

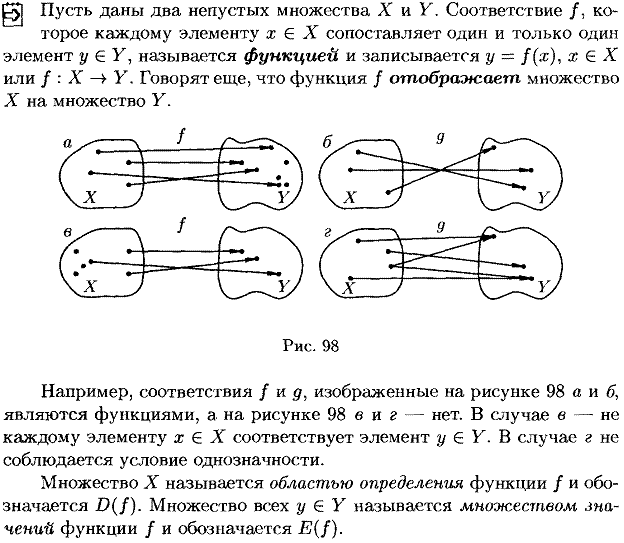
2. Дайте определения функции, области её определения, множества значений и графика, укажите основные способы задания функции, проиллюстрируйте геометрически, приведите примеры.

3. Дайте определения четной (нечетной) и периодической функции, проиллюстрируйте геометрически, приведите примеры.

4. Дайте определения ограниченной (неограниченной) и монотонной функции, проиллюстрируйте геометрически, приведите примеры.

5. Дайте определения числовой последовательности и её предела, проиллюстрируйте геометрически, приведите примеры.

6. Дайте определения предела и односторонних пределов функции в точке, проиллюстрируйте геометрически, приведите примеры.

7. Сформулируйте основные теоремы о пределах функций.

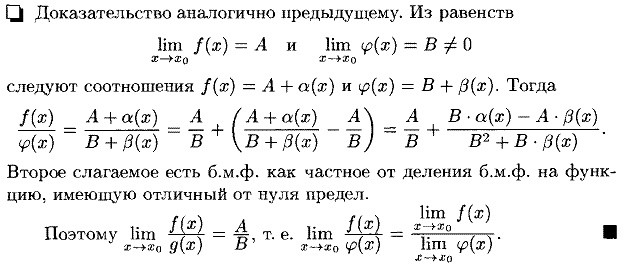
8. Дайте определения бесконечно малой величины и бесконечно малой в точке функции, сформулируйте теоремы об их свойствах, приведите примеры.

9. Дайте определения бесконечно большой величины и бесконечно большой в точке функции, сформулируйте теоремы об их свойствах, приведите примеры.

10. Сформулируйте правила сравнения бесконечно малых и теорему о применении эквивалентных бесконечно малых при вычислении пределов функций. Приведите примеры.

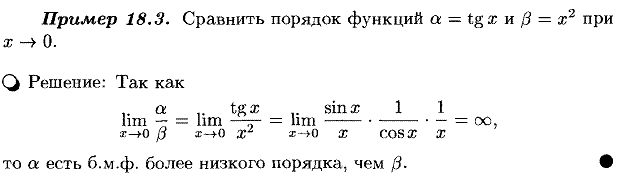
11. Сформулируйте первый и второй замечательные пределы, приведите примеры применения замечательных пределов при вычислении пределов функций.

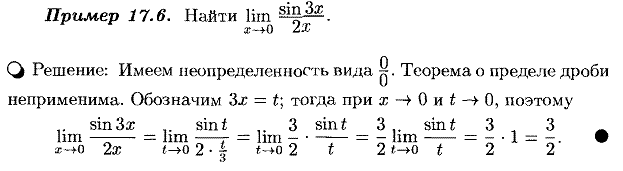
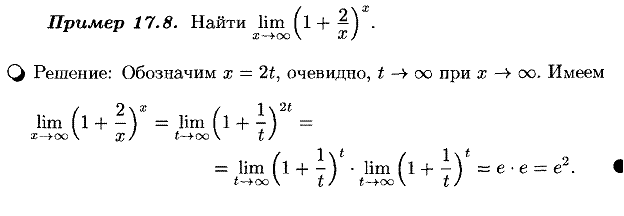
12. Дайте определения непрерывной в точке и на множестве функции, сформулируйте правила действий над непрерывными функциями. Приведите примеры.

13. Проведите классификацию точек разрыва функции, проиллюстрируйте геометрически. Приведите примеры.

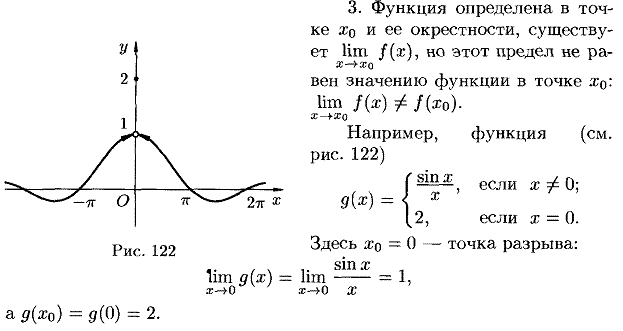
14. Сформулируйте теоремы о свойствах функций, непрерывных на отрезке, проиллюстрируйте геометрически.

15. Дайте определения дифференцируемости функции в точке и на множестве, проиллюстрируйте геометрически и физически.

16. Дайте определение производной первого порядка функции в точке, проиллюстрируйте геометрически. Сформулируйте правила действий над производными функций.

17. Дайте определение сложной функции, сформулируйте теоремы о непрерывности и производной сложной функции, приведите примеры.

18. Дайте определение обратной функции, сформулируйте теорему о производной обратной функции, приведите примеры.

19. Сформулируйте правила Лопиталя для раскрытия неопределенных выражений при вычислении пределов функций. Приведите примеры.

20. Дайте определения производной и дифференциала функции в точке высших порядков, приведите примеры.

21. Сформулируйте основные теоремы о дифференцируемых функциях. Проиллюстрируйте геометрически.

22. Дайте определение первообразной функции, проиллюстрируйте геометрически. Сформулируйте теорему о свойстве первообразных одной функции. Приведите примеры.

23. Дайте определение неопределенного интеграла, проиллюстрируйте геометрически. Сформулируйте основные свойства неопределенного интеграла и теорему существования. Приведите примеры.

24. Сформулируйте теоремы об основных методах интегрирования. Приведите примеры применения метода замены переменной (подстановки) и формулы интегрирования по частям для нахождения неопределенного интеграла.

25. Опишите основные приемы интегрирования рациональных функций. Приведите примеры.

26. Опишите основные приемы интегрирования тригонометрических функций. Приведите примеры.

27. Опишите основные приемы интегрирования иррациональных функций. Приведите примеры.

28. Дайте определение определённого интеграла Римана. Проиллюстрируйте геометрически. Сформулируйте необходимое и достаточное условия интегрируемости функции на отрезке.

29. Сформулируйте теоремы об основных формулах вычисления определенного интеграла. Приведите примеры.

30. Сформулируйте основные свойства определённого интеграла.

31. Запишите формулы для вычисления площади криволинейной трапеции, плоской области и полярного сектора. Проиллюстрируйте геометрически. Приведите примеры.