Интегрирование по частям

Интегрирование по частям

Формула интегрирования по частям имеет следующий вид:

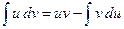Этой формулой обычно пользуются, когда подынтегральное выражение 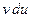проще, чем подынтегральное выражение .

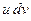Пример:

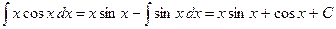
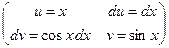
Замечание. При нахождении 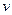не пишут промежуточную произвольную постоянную 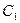, так как она не оказывает влияния на окончательный результат.

Пример:

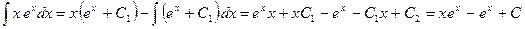
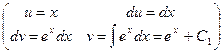
Правило интегрирования по частям применяется во многих случаях, например, для интегралов вида

, ,

, , ,

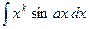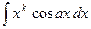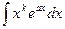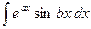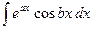а также для некоторых интегралов, содержащих логарифмическую, обратные тригонометрические функции и корни.