Балансовые модели

Для анализа планирования пропорций выпуска и затрат продукции и многоотраслевых народнохозяйственных объектах используются балансовые модели.

Объекты моделирования здесь могут быть различными экономика предприятия, региона, отдельной страны, группы стран.

Первую в мире балансовую модель разработал французский экономист, основоположник школы физиократов, лейб-медик короля Людовика XV Франсуа Кенэ. Это было первое применение математики в экономике. Идея количественного исследования пропорций производства и потребления продукции нашла своё отражение в теории прибавочной стоимости К. Маркса.

Для анализа функционирования народного хозяйства балансовую модель впервые применили в начале 20-х годов советские экономисты, а в начале 30-х годов американец В. В. Леонтьев создал и исследовал балансовую модель, носящую его имя.

Экономическая схема балансовой модели.

Межотраслевой баланс в денежном выражении схематично можно представить в виде таблицы, состоящей из четырёх разделов.

Отрасль материального производства		Производственное потребление отраслей материального производства	Итого	Конечный продукт Y	Валовая продукция X
Производящие отрасли	. i . n	X11 X12 … X1j … X1n X21 X22 … X2j … X2n . . . . … Iраздел(квадрант) . . . . . . Xn1 Xn2 … Xnj … Xnn	D1 D2 Dn	Y1 x1 Y2 x2 II раздел (квадрант) Ynxn
Итого
Амортизация и оплата труда Национальный доход Валовая продукция		V1 V2 Vn IIIраздел (квадрант) M1 M2 Mn X1 X2 Xn		Перераспределительные Процессы IVраздел (квадрант)

Основу баланса составляет I раздел (квадрант)- шахматная таблица, характеризующая межотраслевые связи, строки и столбцы которой соответствуют отраслям межотраслевого производства. В каждой строке показывается распределение производственной продукции, в каждом столбце – затраты на производство соответствующей отрасли. То есть I раздел (квадрант) межотраслевого баланса характеризует межотраслевые поставки сырья, материалов, топлива, электроэнергии, обусловленные производственной деятельностью отраслей материального производства. Показатели этого раздела характеризуют простое производство.

Во II разделе представлены натурально-вещественная структура национального дохода возмещение основных фондов. В I и II разделах отражены общественные потребности в продукции отраслей на производственное и конечное потребление.

III раздел включает условно чистую и валовую продукцию. Условно чистая продукция каждой отрасли разделяется на амортизационные отчисления и национальный доход, включающий заработную плату и прибыль. Данные IIIраздела нужны для анализа структуры и пропорций вновь созданной и перенесенной стоимостей, необходимого и прибавочного продукта в целом по материальному производству и в отраслевом разрезе.

IV раздел отражает конечное распределение национального дохода – перераспределительные процессы.

Итак, основу схемы межотраслевого баланса составляют данные о межотраслевых поставках сырья и материалов. Их запись в виде строки и столбца в таблице межотраслевого баланса, дополненная сведениями о конечных результатах деятельности отраслей, позволяет объединить две записи в бухгалтерских счетов по каждой отрасли – кредит и дебет – в компактную, удобную для обозрения и анализа в таблице. По строкам в ней показано, для каких целей изготовлена продукция – для внутрипроизводственного или конечного потребления, по столбцам – основные платежи, связанные с выпуском продукции.

Перейдём к построению математической модели и экономической схемы межотраслевого баланса производства и распределения продукции в народном хозяйстве.

Балансовая модель предназначена для моделирования таких объектов экономики, зависимость которых от внешней среды выражается в использовании ресурсов, т. е. средств производства, в рамках данного объекта не производимых как продукция. Следовательно, моделируемый объект требует тщательной координации работы отдельных объектов народного хозяйства.

Балансовая модель применима для любого объекта экономики, а также для экономики государств, сильно зависящих от импорта средств производства.

Часть объекта, связанная с выпуском одного вида продукции, называется отраслью. Каждый вид продукции выпускается только одной отраслью. Общее количество отраслей совпадает с количеством видов продукции n.

Интенсивность функционирования отрасли определяется общим количеством продукции Xi, I= 1, n (валовым выпуском), производимой в единицу времени.

Вектором интенсивности (или вектором валового выпуска) назовем вектор X=(x1, x2, …Xn)ᵞ, компоненты которого – интенсивности соответствующих отраслей.

Часть валового выпуска тратится на производственные нужды внутри данного объекта (производственные затраты)

Вектор производственных затрат

D= (D1, D2, …Dn)ᵞ.

Где Di – производственные затраты продукции i отрасли.

Количество продукции i отрасли, затрачиваемое в единицу времени на производственные нужды jотраслью, назовем абсолютными затратами Xij, (i, j=1, n).

Матрица X=(Xij) называется матрицей абсолютных затрат

Справедливо соотношение Di = 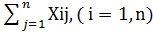. (1)

Каждая отрасль одновременно и производящая и потребляющая.

Превышение валового выпуска по сравнению с производственными затратами называется конечным или чистым выпуском.

Вектор конечного выпуска обозначим

Y= (Y1, Y2, …Yn)ᵀ, где Yi- конечный выпуск i отрасли.

Равенство X=D+Y (2)

Называется основным балансовым соотношением.

Производственные затраты продукции i отрасли на выпуск единицы валовой продукции j отрасли называются коэффициентами прямых затрат и обозначаются Aij, (i, j= 1, n).

Матрица A=(Aij), элементами которой являются коэффициенты прямых затрат, называется матрицей прямых затрат. Диагональные элементы матрицы прямых затрат обязательно должно быть строго меньше единицы.

Пусть всегда справедлива равенства

Xij=AijXj, (i, j=1, n), (3)

Что можно сформулировать следующим образом: производственные затраты продукции всегда пропорциональны валовому выпуску (интенсивности) потребляющей отрасли. Для небольших изменений интенсивности это условие выполняется достаточно точно.

Поставим (3) в (1), получим

Di=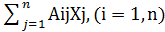

Или в матричной форме D=AX.

Запишем основное балансовое соотношение с учётом (2)

X=AX+Y

Разрешая относительноY, имеем:

Y=X-AX=(E-A)X,

Где E – единичная матрица.

Элементы матрицы (E-A) имеют очевидную экономическую интерпретацию. Если обозначить выпуск продукции положительным числом, т. е. единицей, а затраты – отрицательными, то объединенные нормы «затраты-выпуска» можно записать как матрицу (E-A), которую называют матрицей В. Леонтьева.

Обозначим В= 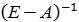. Получим ещё одну форму записи основного балансового соотношения:

X=BY

Данная форма имеет важное практическое значение, поэтому важно выяснить экономический смысл элементов матрицы B=(Bij), называемой матрицей полных затрат.

В результате умножения матрицы В на вектор конечного выпуска получим вектор валового выпуска

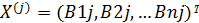, совпадающий с j столбцом матрицы полных затрат, т. е. по конечному продукту Y можно сразу выяснить соответствующие валовые выпуски отраслей. В этом ведущая идея применения межотраслевых моделей для планирования производства.

Если матрица В не имеет отрицательных элементов, то этого достаточно, чтобы моделируемый многоотраслевой объект был эффективным. Если указанное условие выполняется, то соответствующая матрице В матрица А называется продуктивной.

Можно сказать, что право на существование имеют лишь такие объекты, матрица прямых затрат А которых продуктивна. Это имеет важное значение при построении балансовых моделей для проверки достоверности исходных данных.

По приращениям конечного продукта можно найти приращение валовых объемов выпуска:

Δ X=BΔ Y

Потребность всех отраслей в ресурсах может быть охарактеризована матрицей коэффициентов прямых затрат ресурсов М. Можно найти матрицу коэффициентов полных затрат ресурсов S=MB.

Измерение количества труда, содержащегося в продукте, - одна из задач экономической науки. Вложенный в продукт труд – основа его оценки. Известно, что затраты труда, необходимые для производства единицы продукции, складываются из затрат живого и овеществленного труда. Совокупные его затраты в единице продукции имеют важное значение для определения: цен на продукцию, производительности труда и эффективности расширенного воспроизводства.

В качестве исходных параметров для расчета полных затрат труда рассмотрим отчётный баланс в натуральном выражении. В простейшем случае затраты труда будем представлять в единицах труда одинаковой стоимости. Пусть Lj – затраты живого труда в производстве Xj единиц j-го продукта. Тогда прямые затраты труда на единицу j-го вида продукции:

Tj=Lj/xj

Обозначим через Tj полные затраты живого и овеществлённого труда на единицу n-го продукта. Поскольку Aij - затраты i-го продукта в натуральных единицах на единицу j-го продукта, то произведение AijT, отражает затраты овеществленного труда, перенесенного на j-й продукт через i-е средство производства.

T’=TBT’Y=TX

Полные затраты труда на производство вектора конечного продукта Н совместны с прямыми затратами труда на соответствующий вектор валовых выпусков Х.

Труд – источник всех благ, он приводит в движение все производство, все его звенья на всех стадиях. Итого этого – конечный продукт.