Большинство задач на совместную работу можно решить с помощью дробного рационального уравнения. Для решения более сложных задач составляют систему уравнений.

Продолжаем решать задачи на работу!

Внимательно изучите содержание файла.

Задачи на совместную работу

Рассмотрим типичные задачи на совместную работу из курса алгебры 8-9 классов. Решение таких задач начинается с того, что принимаем всю работу за единицу.

Как и другие задачи на работу, задачи на совместную работу связывают время работы, производительность труда и время работы соотношением:

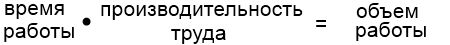
Чаще всего за x принимают время работы, а производительность труда выражают через x.

И еще одна задача на совместную работу.

Так же, как на прошлом уроке, переписать условие и решение задачи, потом решить по аналогии № 721

Один насос может наполнить бассейн на 24 часа быстрее, чем другой. Через 8 часов после того, как был включен второй насос, включили первый, и через 20 часов совместной работы оказалось, что заполнено 2/3 бассейна. За сколько часов может наполнить бассейн каждый насос, работая самостоятельно?

Решение:

Примем весь бассейн за 1. Пусть I насос, работая самостоятельно, может наполнить весь бассейн за x часов, тогда II — за x+24 часа.

	Время работы	Производительность труда	Объем работы
I насос	x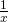
II насос	x+24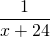

Известно, что II насос был включен 8+20=28 часов, а I — 20 часов, и за это время они наполнили 2/3 бассейна. Составим и решим уравнение:

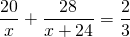
Обе части уравнения делим почленно на 2 и переносим все слагаемые в левую часть:

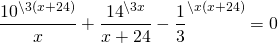
ОДЗ. Х не равен 0; х не равен -24.

30х + 720 + 42х –х² – 24х = 0

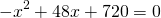
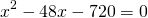
Решить через дискриминант

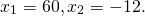
Второй корень — посторонний.

Значит, I насос может наполнить бассейн самостоятельно за 60 часов,

а II — за 60+24=84 (часа)

Ответ: за 60 часов и 84 часа.

Конец формы