
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Равномерное распределение
Равномерное распределение
Распределение вероятностей непрерывной случайной величины X, принимающей все значения из отрезка [a; b], называется равномерным, если её плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т. е.
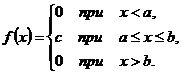
Так как 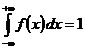 , получаем
, получаем 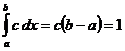 , отсюда
, отсюда 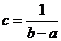 .
.
Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [a; b], имеет вид:
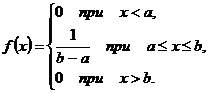

Определим математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины с равномерным распределением.
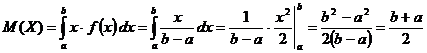 .
.
Таким образом, 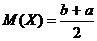 , как и должно, быть в силу симметрии распределения.
, как и должно, быть в силу симметрии распределения.
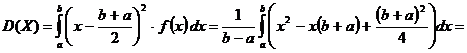
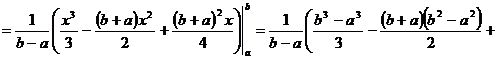
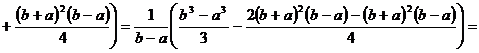
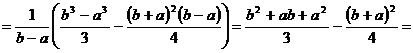
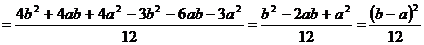 .
.
Таким образом, 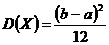 , тогда
, тогда 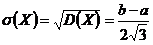 .
.
Пример. Все значения равномерно распределённой случайной величины лежат на отрезке [2; 8]. Найти вероятность попадания случайной величины в промежуток (3; 5).
a=2, b=8, 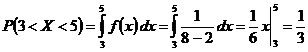 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|