
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Параллельные прямые. Подобные треугольники.
Параллельные прямые
Две прямые AB и CD называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать (AB|| CD). Угол между параллельными прямыми равен нулю.
Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, - расстояние между ними.
Аксиома: через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Свойства параллельных прямых:
1. Если две прямые параллельны третьей прямой, то они параллельны между собой.
2. Если две прямые перпендикулярны третьей прямой, то они параллельны друг другу.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис. 13 ), которые попарно называются:
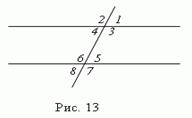
1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 );
углы попарноравны: ( 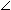 1 =
1 = 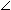 5;
5; 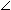 2 =
2 = 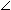 6;
6; 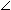 3 =
3 = 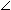 7;
7; 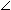 4 =
4 = 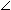 8 );
8 );
2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); сумма односторонних углов равна 180 °
( 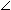 3 +
3 + 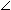 5 = 180°;
5 = 180°; 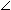 4 +
4 + 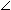 6 = 180° );
6 = 180° );
5) внешние односторонние углы ( 1 и 7; 2 и 8 ); их сумма равна 180° ( 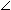 1 +
1 + 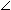 7 = 180°;
7 = 180°; 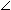 2 +
2 + 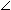 8 = 180°).
8 = 180°).
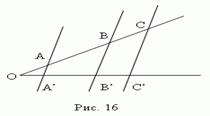
Теорема Фалеса. При пересечении сторон угла параллельными прямыми ( рис. 16 ) стороны угла делятся на пропорциональные отрезки:
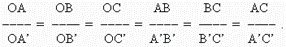
Подобные треугольники.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Сходственные стороны подобных треугольников — это стороны, лежащие напротив равных углов.
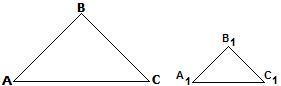
Два треугольника подобны, если 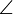 A =
A = 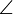 A1,
A1, 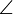 B =
B = 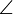 B1,
B1, 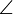 С =
С = 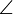 С1 и
С1 и 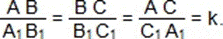 Число k, равное отношению сходственных сторон треугольника называется коэффициентом подобия.
Число k, равное отношению сходственных сторон треугольника называется коэффициентом подобия.
Признаки подобия:
1. Если два угла одного треугольника соответственно равны двум углам другого, то треуг-ки подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Следствия: 1. Площади подобных треугольников относятся как квадрат коэффициента подобия:
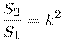 2. Отношение периметров подобных треугольников и биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
2. Отношение периметров подобных треугольников и биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
|
|

 Высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:
Высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы: 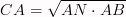
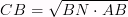
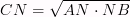
|
| ||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|