Геометрия 10 класс. Тема: «Усеченная пирамида». Теория. Sполн.усеч .= Sбок + Sверхн.осн. + Sнижн.осн. = Sбок + S+ s

Геометрия 10 класс

Урок № 3 (14. 04. 20)

Тема: «Усеченная пирамида»

Теория

УСЕЧЕННАЯ ПИРАМИДА

Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один из них является пирамидой, а другой называется усечённой пирамидой.

Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды.

Многоугольники АВСD и А₁В₁С₁D₁ – нижнее и верхнее основания усечённой пирамиды

Отрезки АА₁, ВВ₁, СС₁, DD₁ – боковые ребра усечённой пирамиды

Четырёхугольники АА₁В₁В; АА₁D₁D и т. д – боковые грани усечённой пирамиды. Все они являются трапециями.

Отрезок ОО₁ – перпендикуляр, проведённый из какой-нибудь точки верхнего основания к нижнему основанию – называется высотой усечённой пирамиды.

Площадь боковой поверхности (S_бок) – сумма площадей боковых граней (трапеций)

Площадь полной поверхности – сумма площадей всех граней:

Sполн. усеч. = Sбок + Sверхн. осн. + Sнижн. осн. = Sбок + S+ s

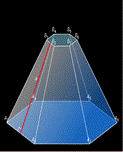ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА

Усеченная пирамида правильная, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Апофема – высота боковой грани правильной пирамиды (высоты трапеций).

1) Основания – правильные многоугольники;

2) Боковые грани – равные равнобедренные трапеции;

3) Имеем несколько пар подобных треугольников: DA₁SD₁¥ DASD и т. д. Þ = = 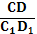= = 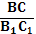= 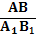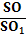k.

Площадь боковой поверхности для правильной усеченной пирамиды:

12 Следующая ⇒