ЗАДАНИЯ по ПАРЕТО-ЭФФЕКТИВНОСТИ

ЗАДАНИЯ по ПАРЕТО-ЭФФЕКТИВНОСТИ

8. 1. 4. В экономике обмена, , где, .

а) Выведите уравнение контрактной линии L и постройте ее в диаграмме Эджворта.

б) Выведите уравнение эффективной границы 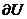множества достижимых полезностей 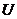и постройте 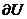и 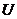в критериальном пространстве 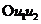экономики обмена.

8. 1. 6. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)^1/3(y₁)^1/3, U₂ = (x₂)^1/3(y₂)^1/3, где х₁ и у₁ - количества продуктов

Х и Y, потребляемые первым потребителем, х₂ и у₂ - количества продуктов Х и Y, потребляемые вторым потребителем. Количество продуктов в экономике ограничено:

Х = х₁ + х₂ = 80, Y = у₁ + у₂ = 30. Определите отношение цен (Рх/Ру) для оптимальных по Парето распределений продуктов Х и Y.

8. 1. 7. Допустим, в экономике производится только два продукта X и Y. При производстве этих продуктов используются два производственных ресурса: капитал (К) и труд (L), количества которых ограничены. Известно, что кривая производственных возможностей (кривая продуктовой трансформации) этой экономики описывается следующим уравнением в пространстве продуктов: 16Х⁴ + Y⁴ = 81.

Определите предельную норму трансформации для производимых продуктов

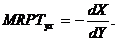
8. 1. 8. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)^2α(y₁)^2α, U₂ = (x₂)^α(y₂)^α, где х₁ и у₁ - количества продуктов

х₁ + х₂ = а₁, у₁ + у₂ = а₂.

1) Выведите уравнение границы достижимых полезностей.

2) Постройте график границы достижимых полезностей при α = 1/4, а₁ = 8, а₂ = 2.

3) Постройте график границы достижимых полезностей при α = 3/4, а₁ = 4, а₂ = 1.

8. 1. 9. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)²y₁, U₂ = x₂y₂, где х₁ и у₁ - количества продуктов

Х = х₁ + х₂ = 6, Y = у₁ + у₂ = 9.

1) Является ли следующее распределение продуктов между двумя потребителями: х₁ = 3, y₁ = 6, x₂= 3, y₂ = 3 эффективным по Парето?

2) Постройте диаграмму Эджуорта и кривые безразличия обоих потребителей, проходящие через точку заданного распределения (см. 1)).

3) Найдите контрактную линию и переговорное множество.

4) Найдите эффективное по Парето распределение продуктов, при котором достигается максимум полезности первого потребителя при начальном уровне полезности второго.

5) Оцените изменение полезности первого потребителя при переходе из точки начального распределения в точку эффективного распределения продуктов, найденную в 4).

6) Чему равны предельные нормы замещения в точке эффективной по Парето из 4).

8. 1. 10. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)²y₁, U₂ = 3x₂(y₂ – 2) где х₁ и у₁ - количества продуктов

Х = х₁ + х₂ = 4, Y = у₁ + у₂ = 10.

1) Является ли следующее распределение продуктов между двумя потребителями: х₁ = 2, y₁ = 3, x₂= 2, y₂ = 7 эффективным по Парето?

2) Постройте диаграмму Эджуорта и кривые безразличия обоих потребителей, проходящие через точку заданного распределения продуктов (см. 1)), отразите на графике предельные нормы замещения продуктов обоих потребителей в точке заданного распределения продуктов.

3) Найдите контрактную линию, изобразите ее на диаграмме Эджуорта.

4) Найдите эффективное по Парето распределение продуктов, при котором достигается максимум полезности второго потребителя при начальном уровне полезности первого.

5) Оцените изменение полезности второго потребителя при переходе из точки начального распределения в точку эффективного распределения продуктов, найденную в 4).

6) Чему равны предельные нормы замещения в точке эффективной по Парето из 4).

8. 1. 12. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)²y₁, U₂ = x₂y₂, где х₁ и у₁ - количества продуктов

Х = х₁ + х₂ = 4, Y = у₁ + у₂ = 10.

1) Является ли следующее распределение продуктов между двумя потребителями:

х₁= 2, y₁ = 4, x₂= 2, y₂ = 6, эффективным по Парето?

3) Найдите контрактную линию и переговорное множество.

6) Найти отношение предельных полезностей для обоих потребителей в точке эффективной по Парето из 4).

8. 1. 13. Рассматриваются две фирмы, одна из которых производит продукт Х, другая – продукт Y. Обе фирмы используют одни и те же ресурсы – труд (L) и капитал (К), запасы которых ограничены и составляют L = 6, К = 96. Известны производственные функции фирм, отражающие производство продуктов: X = L₁^3/4K₁^1/4 и Y = L₂^3/4K₂^1/4.

1) Определите, является ли распределение ресурсов L₁= 5, K₁= 55; L₂= 1, K₂= 11 оптимальным по Парето.

2) Найдите одно из оптимальных по Парето распределений ресурсов между фирмами, для которого доcтигается максимум выпуска продукта Х при производстве Y =3.

3) Приведите геометрическую интерпретацию решения:

3. 1) изобразите коробку Эджуорта и начальное распределение ресурсов согласно 2);

3. 2) постройте график контрактной линии;

3. 3) проведите изокванты: для продукта Y, проходящую через точку L₂= 1, K₂= 11 и для продукта Х, проходящую через точку L₁= 5, K₁= 55;

3. 4) выделите на контрактной линии переговорное множество;

3. 5) изобразите на графике предельные нормы технического замещения для обеих фирм в точке начального распределения песурсов;

3. 6) отметьте найденное в 2) эффективное по Парето распределение ресурсов.

4) выведите уравнение границы производственных возможностей.

8. 1. 15. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)^1/2(y₁)^1/2, U₂ = (x₂)^1/2(y₂)^1/2,

где х₁ и у₁ - количества продуктов Х и Y, потребляемые первым потребителем, х₂ и у₂ - количества продуктов Х и Y, потребляемые вторым потребителем. Количество продуктов в экономике ограничено: Х = х₁ + х₂ = 100, Y = у₁ + у₂ = 64. Известно исходное распределение продуктов Х и Y между потребителями: (х₂, у₂) = (64; 49).

Найдите одно из оптимальных по Парето распределений продуктов Х и Y между потребителями, при котором достигается максимум полезности первого потребителя, а уровень полезности второго остается без изменений (соответствует исходному распределению).

8. 1. 16. Допустим, в экономике существуют два потребителя и два продукта: X и Y.

Функции полезности потребителей имеют следующий вид:

U₁ = (x₁)^1/2(y₁)^1/2, U₂ = (x₂)^1/2(y₂)^1/2,

где х₁ и у₁ - количества продуктов Х и Y, потребляемые первым потребителем, х₂ и у₂ - количества продуктов Х и Y, потребляемые вторым потребителем. Количество продуктов в экономике ограничено: Х = х₁ + х₂ = 48, Y = у₁ + у₂ = 27. Известно исходное распределение продуктов Х и Y между потребителями: (х₁, у₁) = (9; 36).

Найдите одно из оптимальных по Парето распределений продуктов Х и Y между потребителями, при котором достигается максимум полезности второго потребителя, а уровень полезности первого остается без изменений (соответствует исходному распределению).