Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

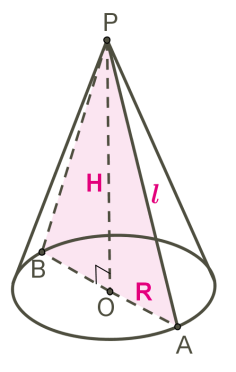
Треугольник POA вращается вокруг стороны PO.

PO — ось конуса и высота конуса.

P — вершина конуса.

PA — образующая конуса.

Круг с центром O — основание конуса.

AO — радиус основания конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось PO конуса.

Осевое сечение конуса — это равнобедренный треугольник.

APB — осевое сечение конуса.

∡ PAO=∡ PBO — углы между образующими и основанием конуса.

Развёрткой боковой поверхности конуса является круговой сектор. Длина дуги сектора — это длина окружности основания конуса длиной 2π R, угол развёртки боковой поверхности α.

В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.

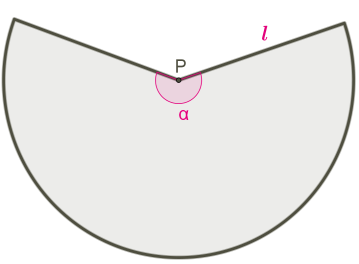
Радиус сектора — это образующая конуса.

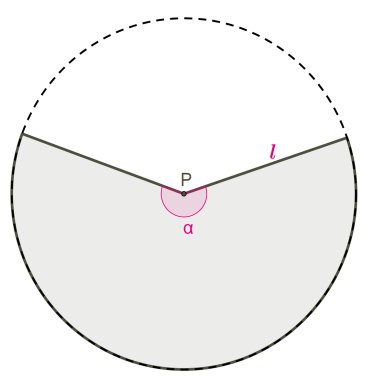
Таким образом, боковая поверхность конуса является частью полного круга с радиусом l:

Sбок. =π l2⋅ α 360°.

Длина дуги также является частью длины полной окружности с радиусом l, но в то же время длина дуги — это длина окружности основания конуса с радиусом R.

Сравним выражения длины дуги и выразим α через R:

2π l⋅ α 360°=2π R; α =2π R⋅ 360°2π l=R⋅ 360°l.

Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:

Sбок. =π l2⋅ R⋅ 360°360°⋅ l=π Rl.

Усечённый конус

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

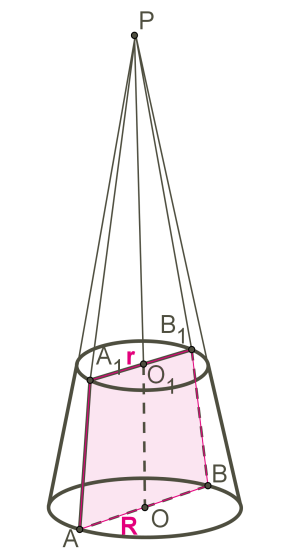
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

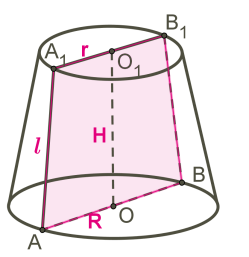
OO1 — ось конуса и высота конуса.

AA1 — образующая конуса.

Круги с центрами O и O1 — основания усечённого конуса.

AO и A1O1 — радиусы оснований конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось OO1 конуса.

Осевое сечение конуса — это равнобедренная трапеция.

AA1B1B — осевое сечение конуса.

Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:

Sбок. =π R⋅ PA− π r⋅ PA1=π R⋅ (PA1+AA1)− π r⋅ PA1==π R⋅ PA1+π R⋅ AA1− π r⋅ PA1==π R⋅ l+(π R− π r)⋅ PA1.

Так как Δ PAO∼ Δ PA1O1, то стороны их пропорциональны:

PAPA1=Rr; l+PA1PA1=Rr; r⋅ (l+PA1)=R⋅ PA1; rl=R⋅ PA1− r⋅ PA1; PA1⋅ (R− r)=rl; PA1=rlR− r.

Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:

Sбок. =π Rl+π ⋅ PA1⋅ (R− r)=π Rl+π ⋅ rlR− r⋅ (R− r); Sбок. =π Rl+π rl=π l⋅ (R+r