Конспект урока. Математика6 класс. Бесконечные периодические десятичные дроби. Теоретический материал для самостоятельного изучения

Конспект урока

Математика6 класс

Бесконечные периодические десятичные дроби

Перечень рассматриваемых вопросов:

– понятие бесконечной периодической десятичной дроби;

– преобразование обыкновенных дробей в бесконечные периодические дроби;

– действия с периодическими дробями.

Бесконечная периодическая десятичная дробь – это дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодоми записывается в скобках.

Любое рациональное число p/q можно разложить в периодическую десятичную дробь.

Любая периодическая дробь есть десятичное разложение некоторого рационального числа.

Теоретический материал для самостоятельного изучения

Обыкновенную дробь можно разложить в конечную десятичную, если в знаменателе нет простых множителей, кроме 2 и 5.

Вы уже знаете, как это сделать.

1. Умножить числитель и знаменатель на одно и то же число, чтобы привести к знаменателю 10, 100, 1000 и т. д.;

2. Выполнить деление числителя на знаменатель.

Пример 1. Умножили числитель и знаменатель на 2.

Пример 2. Сначала сократили дробь.

Пример 3. Выполнили деление 3 на 125.

Рассмотрим примеры, когда привести к знаменателю 10, 100 и т. д. нельзя. Возможно только деление числителя на знаменатель.

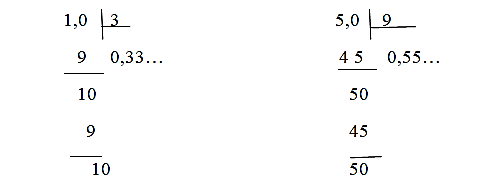
Заметим, что при делении получаются повторяющиеся остатки и, соответственно, повторяющиеся цифры в частном. Из-за этого процесс деления бесконечен. Отсюда происходит бесконечная десятичная дробь.

Рассмотрим другие примеры.

Повторяющиеся цифры 3; 27; 6 называют периодом дроби. Бесконечные десятичные дроби 0, 333…; 0, 2727…; 0, 1666… называют периодическими.

Записывают так:

0, (3)

0, (27)

0, 1(6)

Читают так:

«Нуль целых и три в периоде»

«Нуль целых и 27 в периоде»

«Нуль целых одна десятая и шесть в периоде»

Периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или несколько цифр (период дроби).

Отметим, что любое рациональное число p/q разлагается в периодическую десятичную дробь.

Любая периодическая дробь есть десятичное разложение некоторого рационального числа.

Замечание. При делении уголком десятичное разложение с периодом 9 не возникает.

Далее рассмотрим, как выполняются действия с периодическими дробями?

1. Сравните дроби

1/3 и 0, 3

Запишем дробь 1/3 в виде бесконечной периодической дроби 0, 333…

Запишем дробь 0, 3 в следующем виде 0, 300… Приписывая бесконечно много нулей, мы превращаем конечную дробь в равную ей бесконечную периодическую дробь с периодом 0.

Теперь можем сравнить: 0, 333… > 0, 300…

2. Разложите обыкновенную дробь в бесконечную периодическую десятичную дробь, округлите до десятых.

1/3 = 0, 333… ≈ 0, 3

5/9 = 0, 555… ≈ 0, 6