
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Описание метода

Содержание:
Введение……………………………………………………………………….. 3
1. Исходные данные……………………………………………………5
2. Структурный и кинематический анализ механизма………………6
2. 1. Структурный анализ механизма…………………………….. 6
2. 2. Кинематический анализ механизма…………………………8
2. 2. 1. Графический метод…………………………………………... 8
2. 2. 2. Графоаналитический метод анализа с применением численного дифференцирования………………………………………9
3. Синтез зубчатого механизма…………………………………….... 13
3. 1 Кинетический расчет трансмиссии привода ………………... 13
3. 2 Расчет элементов зубчатой пары …………………………….. 15
3. 3 Качественные показатели зацепления ………………………. 18
4. Синтез кулачкового механизма ……………………………………. 20
Литература……………………………………………………………... 24
Введение
Одной из ведущих отраслей современной техники является машиностроение. По уровню развития машиностроения судят о развитии производительных сил в целом. Прогресс машиностроения в свою очередь определяется созданием новых высокопроизводительных и надёжных машин. Решение этой важнейшей проблемы основывается на комплексном использовании результатов многих дисциплин и, в первую очередь, теории механизмов и машин.
Теория механизмов и машин - наука об общих методах исследования свойств механизмов и машин и проектировании их схем.
Качество создаваемых машин и механизмов в значительной мере определяется полнотой разработки и использования методов ТММ. Чем более полно будут учтены при построении механизмов и машин критерии производительности, надёжности, точности и экономичности, тем совершеннее будут получаемые конструкции.
В данном курсовом проекте требуется спроектировать и произвести кинематический и кинетостатический расчёт поперечно-строгального станка.
Рационально спроектированная машина должна удовлетворять социальным требованиям - безопасности обслуживания и создания наилучших условий для обслуживающего персонала, а также эксплуатационным, экономическим, технологическим и производственным требованиям. Эти требования представляют собой сложный комплекс задач, которые должны быть решены в процессе проектирования нового механизма.
Решение этих задач на начальной стадии проектирования состоит в выполнении анализа и синтеза проектируемого механизма, а также в разработке его кинематической схемы, обеспечивающей с достаточным приближением воспроизведение требуемого закона движения.
В первом разделе исследуется кинематика кулисного механизма. Строится план механизма, планы скоростей, планы ускорений, диаграммы перемещения, скорости и ускорения ползуна.
Во втором разделе проводится синтез зубчатого механизма. Определяются параметры зубчатого зацепления и производится его вычерчивание
В третьем разделе производится силовой анализ механизма. Строятся силовые многоугольники. Определяются силы, действующие на механизм по методу последовательного рассмотрения групп Ассура и по методу рычага Жуковского.
В четвертом разделе проводится синтез кулачкового механизма. По диаграмме S(t) определяются основные законы движения кулачка, строится диаграмма теоретического профиля.
В пятом разделе производится расчет маховика.
1. Исходные данные
| Дано | Обозначения | Значения |
| Модуль паланетарной передачи, мм | mI | 2, 5 |
| Модуль зуб. передачи, мм | mII | |
| Размеры звеньев, м | ОА | 0, 15 |
| АВ | 0, 96 | |
| ВС | 0, 53 | |
| BD | 0, 53 | |
| ∆ | 0, 015 | |
| Числа зубьев колес | Z4 | |
| Z5 | ||
| Расстояние между стойками, м | в | 0, 5 |
| Масса звеньев, кг | m2 | |
| m3 | ||
| m4 | ||
| m5 | ||
| Момент инерции, кгм2 | Js1 | 0, 5 |
| Js2 | 1, 5 | |
| Js3 | 0, 6 | |
| Js4 | 0, 6 | |
| φ у+φ д. с. + φ в+φ р, град | φ р | |
| Ход толкателя, м | hmax | 0, 014 |
| Минимальный угол передачи движения, град | γ min | |
| Коэффциент неравномерности хода | δ | 1/15 |
| Число оборотов двигателя в минуту ( nz1) | |
| Передаточное отношение (U1-5) | 22, 5 |
| Зацепление | Z4-Z5 неравносм. |
| Диаграмма ускорения толкателя | Б |
| Qmax, кН |
1. Структурный и кинематический анализ механизма
1. 1. Структурный анализ механизма
Условные обозначения звеньев механизма:
0 – стойка
1 – кривошип ОА
2 – шатун АВ
3 – кривошип ВС
4 – шатун ВD
5 – ползун D
Степень подвижности механизма определяется по формуле:
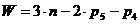 ,
,
где n – количество подвижных звеньев;
p5 – количество кинематических пар 5-го класса;
p4 – количество кинематических пар 4-го класса.
В данном механизме:
n=5;
p5=7;
p4=0.
Кинематические пары: 0-1; 1-2; 2-3; 3-0; 3-4; 4-5; 5-0,
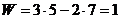
Это подтверждает, что в нашем случае одно ведущее звено.
Относительная степень подвижности присоединяемой группы звеньев к ведущему звену определяется без учета главного звена:
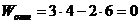
Классификация кинематических пар и групп звеньев в механизме сведены в две таблицы
Таблица 1. - Классификация кинематических пар.
| № п\п | Кинемат. Пара | Наименование | Класс | Кол-во степ. свободы |
| 0-1 | Вращательная | |||
| 1-2 | Вращательная | |||
| 2-3 | Вращательная | |||
| 3-0 | Вращательная | |||
| 2-4 | Вращательная | |||
| 4-5 | Поступательная | |||
| 5-0 | Поступательная |
Таблица 2. - Классификация групп звеньев
| №п/п | Схема группы | Класс группы по Ассуру | Порядок группы |
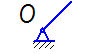
| І | - | |

| ІІ | ||

| ІІ |
На основании таблиц 1 и 2 структурная формула механизма будет выглядеть:
I(0 – 1) – II(2 – 3) – II(4 – 5)
1. 2. Кинематический анализ механизма
1. 2. 1. Графический метод
В масштабе μ =0, 005 м/мм строим план механизма, начиная с построения ведущего звена – кривошипа О1А. Кривошип изображаем в 12-ти положениях через каждые 300, начиная с нулевого положения (т. е. при котором образуется угол 180º между кривошипом ВС и шатуном BD). Для каждого положения кривошипа методом засечек определяем положение всех остальных звеньев механизма.
Планы скоростей будем строить для выбранных произвольно положений механизма.
Последовательность построения плана скоростей и ускорений данного механизма рассмотрим на примере построения этих планов для 1-го положения.
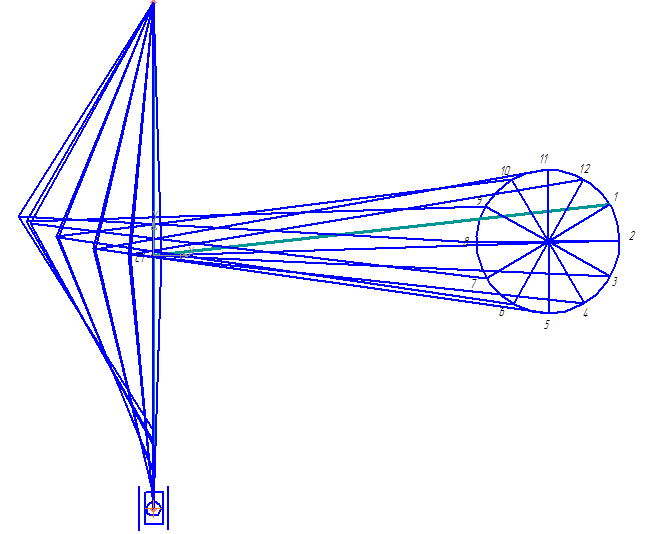
Рис. 2. 1. - Кинематическая схема механизма, изображенная в 12 положениях
1. 2. 2. Графоаналитический метод анализа с применением численного дифференцирования
Исходные данные:
j1=0, 5236(30°) – угол поворота начального звена;
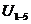 =22, 5– передаточное отношение многозвенной зубчатой передачи;
=22, 5– передаточное отношение многозвенной зубчатой передачи;
 =1125 об/мин – частота вращения электродвигателя.
=1125 об/мин – частота вращения электродвигателя.
Описание метода
Графоаналитическое исследование перемещений, скоростей и ускорений ведется для ряда положений механизма, достаточно близко отстоящих друг от друга. В нашем случае механизм изображаем в 12 положениях. Строятся эти положения в результате деления одного оборота главного звена на 12 равных частей, что показано на чертеже. Построение ведется в заданном масштабе.
 ,
,
где ω 1=π · nОА/30=3, 14·50/30=5, 23м/с² - угловая скорость начального звена;
nОА=nдв/U1-5=1125/22, 5=50 об/мин - частота вращения начального звена.
∆ t=0, 5236/5, 23=0, 1c
Полученные показания перемещения, снятые с чертежа и умноженные на соответствующий масштаб, заносим в пятый столбец таблицы. В девятом и одиннадцатом столбце вводим формулы соответственно для вычисления скорости и ускорения. Эти формулы основаны на дифференцировании перемещения по времени:
 ;
; 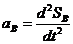
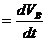 .
.
По полученной таблице строим диаграммы зависимостей Sв(t); Vв(t); aв(t).
Все измерения и полученные результаты сводятся в таблицу 3.
Таблица 3. Результат графоаналитического метода анализа
| N | φ, град | φ, рад | S, мм | S∙ μ l, м | t, с | ∆ S∙ μ l, м | ∆ t, c | V, м/с | ∆ V, м/c | a, м/c² |
| 0, 0000 | 0, 0000 | 0, 0000 | 0, 0000 | 0, 1001 | 0, 0000 | 0, 1577 | 1, 5749 | |||
| 0, 5236 | 0, 6314 | 0, 0158 | 0, 1001 | 0, 0158 | 0, 1001 | 0, 1577 | 0, 3331 | 3, 3274 | ||
| 1, 0472 | 2, 5968 | 0, 0649 | 0, 2002 | 0, 0491 | 0, 1001 | 0, 4908 | -0, 2620 | -2, 6173 | ||
| 1, 5708 | 3, 5129 | 0, 0878 | 0, 3003 | 0, 0229 | 0, 1001 | 0, 2288 | 0, 4920 | 4, 9147 | ||
| 2, 0944 | 6, 3994 | 0, 1600 | 0, 4005 | 0, 0722 | 0, 1001 | 0, 7208 | -1, 0932 | -10, 9197 | ||
| 2, 6180 | 4, 9080 | 0, 1227 | 0, 5006 | -0, 0373 | 0, 1001 | -0, 3724 | 0, 0240 | 0, 2402 | ||
| 3, 1416 | 3, 5129 | 0, 0878 | 0, 6007 | -0, 0349 | 0, 1001 | -0, 3484 | 0, 1516 | 1, 5143 | ||
| 3, 6652 | 2, 7249 | 0, 0681 | 0, 7008 | -0, 0197 | 0, 1001 | -0, 1968 | -0, 3442 | -3, 4381 | ||
| 4, 1888 | 0, 5585 | 0, 0140 | 0, 8009 | -0, 0542 | 0, 1001 | -0, 5410 | 0, 7517 | 7, 5088 | ||
| 4, 7124 | 1, 4025 | 0, 0351 | 0, 9010 | 0, 0211 | 0, 1001 | 0, 2108 | 0, 4370 | 4, 3650 | ||
| 5, 2360 | 3, 9965 | 0, 0999 | 1, 0011 | 0, 0649 | 0, 1001 | 0, 6478 | -0, 5544 | -5, 5376 | ||
| 5, 7596 | 4, 3704 | 0, 1093 | 1, 1013 | 0, 0093 | 0, 1001 | 0, 0934 | -0, 0934 | -0, 9326 | ||
| 6, 2832 | 0, 0000 | 1, 2014 | -0, 1093 | 0, 1001 | 0, 0000 | 0, 1577 | 1, 5749 |
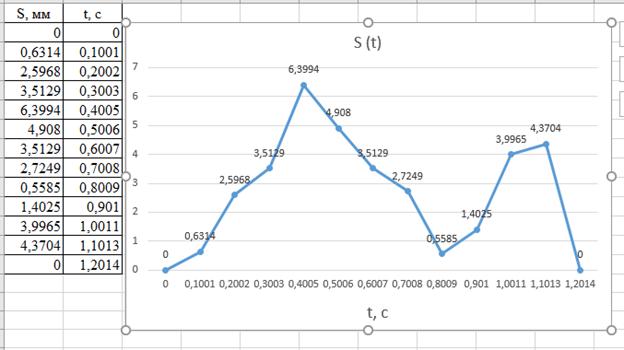
Рис. 2. 2. - Диаграмма зависимости Sв(t);

Рис. 2. 3. - Диаграмма зависимости Vв(t);
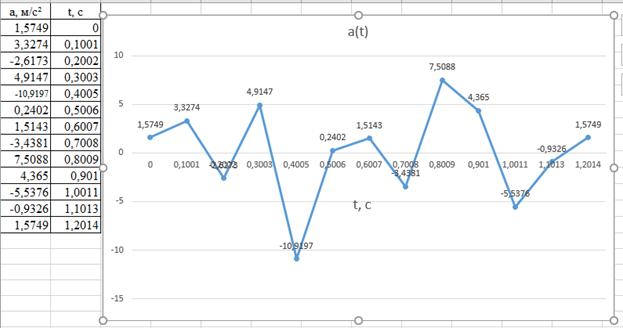
Рис. 2. 4. - Диаграмма зависимости aв(t)
Выводы по результатам кинематического анализа:
Анализируя два, выше разобранных метода, приходим к выводу, что наиболее быстрый и удобный из этих методов – графо – аналитический. Метод имеет незначительную трудоемкость, но вносит в результаты расчетов погрешности, поэтому его можно рекомендовать к использованию только в приближенных расчетах. Графический метод – неточный и неудобный, потому что планы скоростей и ускорений нужно строить на большом формате для уменьшения погрешности.
3. Синтез зубчатого механизма
3. 1Кинематический расчет трансмиссии привода
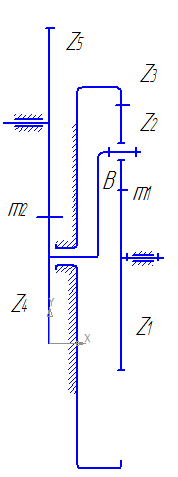
Рис. 3. – Кинематическая схема
U1-5=U1-3·U4-5
Отсюда передаточное отношение между первым колесом и третьим:
U1-3= U1-5/ U4-5
U1-5=22, 5
U4-5=Z5/ Z4=45/13=3, 46
U1-3 = 22, 5/3, 46 = 6, 5
Условия для проверки количества зубьев колес планетарного редуктора:
1.  .
.
2. Соотношения между числами зубьев сателлита исходя из динамических характеристик передачи можно брать равным:
 .
.
3. Из равенства межцентровых расстояний 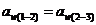 получаем:
получаем:
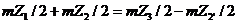 или
или 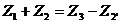 .
.
4. Для того чтобы передачу можно было собрать должно выполняться следующее условие сборки:
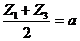 ,
,
где a - целое число.
5. Для уменьшения габаритов редуктора желательно иметь минимальное значение 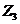 =min,
=min, 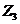 > 85.
> 85.
6. Условие соседства:
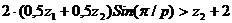
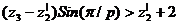
Подбор количества зубьев производится с помощью программы «Project. exe» с учетом условий 1-6.
Вследствие чего получаем: Z1=20, Z2=52, Z3=124, Z2’=52.
Проверка:
1. 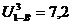
2. Z2/Z2'=1
3. 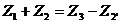
20+52=124-52; 72 = 72
4.  =(20+52)/2,
=(20+52)/2,  - целое
- целое
5. 124> 85
6. 2(10+26)> 54, 72> 54
72> 54.
Почти все условия выполняются (кроме 2), значит подбор числа зубьев осуществлен верно.
3. 2 Расчёт элементов зубчатой пары
Исходные данные: m=11, Z4=13, Z5=45, β =0.
h*а =1, с*=0, 25, α =20°,  , где
, где
h*а - коэффициент высоты головки;
с* - коэффициент радиального зазора;
α - угол профиля;
 - коэффициент радиуса кривизны переходной кривой.
- коэффициент радиуса кривизны переходной кривой.
По таблицам 5 и 6 гл. IV (Кореняко А. С. ) находим для данной зубчатой пары 4-5 коэффициенты смещения x4 и 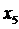 : x4 = 0, 8 и
: x4 = 0, 8 и 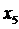 = 0, 635.
= 0, 635.

α t = 0, 364
Расчет элементов зубчатой пары 4-5.
1. Делительные диаметры: d4=mz4/cos β =11*13=143 мм;
d5=mz5/ β =11*45=495 мм.
2. Основные диаметры:
db4=d4·cosα =143* cos20º =134, 37 мм
db5=d5·cosα = 495* cos20º =465, 15 мм
3. Окружной и основной шаги:
P = π *m = 11π = 34, 55
Pb = P*cosα = 32, 47
4. Окружные толщины зубьев (по делительной окружности):
S4=0, 5P+2x4*m*tgα =23, 68
S5=0, 5P+2x5*m*tgα =22, 36
5. Угол зацепления определится из формулы:
іnvα tw=(2(x4+x5)tgα ) / (z4+z5)+ іnvα =((2*1, 758*0, 364)/76)+0, 0149=0, 0329
α tw=25º, 45'
6. Начальные диаметры:
dw4=db4/cosα w=210, 491/ cosα w =142, 9 мм
dw5=db5/cosα w=789, 342/ cosα w =516, 11 мм
7. Межосевое расстояние:
aw=0, 5(dw1+dw2)=318, 95 мм
8. Диаметры впадин:
df4=d4-2(ha*+c*-x4)m=139, 1мм
df5=d5-2(ha*+c*- x5)m=481, 47мм
9. Делительное межосевое расстояние:
а= (z4+z5 )m/2=319
10. Коэффициент воспринимаемого и уравнительного смещения:
y= (aw-a)/m= 1, 24
∆ y= z4+z5 –y=0, 2
11. Диаметры вершин зубьев:
da4=d4+2(ha*+x4-∆ y)m=178, 23 мм
da5 = d5+2(ha*+x5-∆ y)m=526, 6 мм
12. Проверка на заострение (по толщине зубьев на поверхности вершин):
Sa4=da4(S4/ d4+ іnvα - іnvα a4)=133, 1 мм
Sa5=da5(S5/ d5+ іnvα - іnvα a5)=481, 47 мм
Углы α a4 и α a5 определяются из формул:
cos α a4=db4/da4=0, 7538, α a4=4104’
cos α a5=db5/da5=0, 8832, α a5=27050’
13. Длина общей нормали для контроля колеса 6:
W4=(zn4-1)Pb+Sb4
W5=(zn5-1)Pb+Sb5
Здесь расчетное число зубьев в длине общей нормали определяется по формуле:
zn4=z4/9+0, 5,
zn5=z5/9+0, 5,
с округлением до ближайшего большего числа, что обеспечивает положение точек контакта губок штангенциркуля в близи делительной окружности.
Толщину зуба по основной окружности можно найти по формуле:
Sb4=db4(S4/d4+ іnvα ); Sb5=db5(S5/d5+ іnvα )
Получили: zn4=1, 94≈ 2
zn5=5, 5≈ 6
Sb4=210, 491·(31, 967/224+0, 0149)=18, 77
Sb5=789, 342(29, 909/840+0, 0149)=23. 59
W4=(2-1)·32, 47+18, 77=51, 24
W5=(6-1)·32, 47+23, 59=185, 94
14. Шаг зацепления:
t=11*3. 14=34, 55.
Проверка на подрезание:
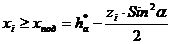 .
.
X4=0, 8, X5=0, 635
Xпод=1-(13·sin² 20º )/2=-0, 26; Xпод=1-(45·sin² 20º )/2=-2, 13
0, 8 ≥ -0, 26; 0, 635 ≥ -2, 13;
Подрезание отсутствует, следовательно, коэффициенты были выбраны верно.
3. 3 Качественные показатели зацепления
1. Коэффициентом перекрытия называют отношение длины К дуги зацепления к длине шага Рв по начальным окружностям колес.
Коэффициент перекрытия, ε, определяющий среднее число пар зубьев, находящихся одновременно в зацеплении, подсчитывают по формуле:
ε =λ АВ/Рв=gα /Рв=51, 24/34, 55=1, 483≈ 1, 5,
где Рв- основной шаг;
λ АВ= gα - истинная длина активной части линии зацепления (фактическая линия зацепления).
Эту длину следует определить с помощью построения.
Радиусы кривизны эвольвент на окружностях выступов равны:
Ра4=0, 5(da42- db42)1/2=58, 55
Ра5=0, 5(da52- db52)1/2=123, 48
gα =ga+gt=Ра4+Ра5-аw*sinα tw=43, 46
Коэффициент перекрытия дает возможность определить число пар профилей зубьев, находящихся одновременно в зацеплении. Для этого нужно воспользоваться теми целыми положительными числами, между которыми находится числовое значение коэффициента перекрытия. Эти целые числа определяют те числа пар профилей зубьев, которые попеременно участвуют в зацеплении. Коэффициент перекрытия не должен быть меньше единицы, так как это приводит к перерывам в передаче движения от ведущего колеса к ведомому и к ударам зубьев колес. При проектировании зацепления коэффициент перекрытия берут не меньше 2, 3 (в данном случае это условие выполняется). Чем больше ε, тем выше качество.
2. Коэффициент удельного скольжения υ характеризует вредное влияние скольжения профилей зубьев, вследствие его появляются силы трения и износ, снижается КПД передачи:
υ 4=Δ Ѕ4- Δ Ѕ5/ Δ Ѕ4 =1-(р5*z4)/(р4/ z5);
υ 5 = Δ Ѕ5- Δ Ѕ4/ Δ Ѕ5 =1-(р4*z5)/(р5/ z4),
где Рр4=аwsinα tw-Ра5=318, 95·sin25º 45'-58, 55=80, 01
Рр5=аwsinα tw-Ра4=318. 95·sin25º 45'-123, 48=15, 07
В точке а4:
υ а4 = 1-(Рр5*z4)/ (Рa4*z5) = 0, 92
В точке P4:
υ р4 = 1-(Ра5*z4)/ (Рр4*z5) = 0, 55
В точке а5:
υ а5 = 1-(Рр4*z5)/ (Рa5*z4) = -1, 24
В точке P5:
υ р5 = 1-(Ра4*z5)/ (Рр5*z4) = -12, 44
3. Коэффициент удельного давления q пропорционален величине напряжения сжатия на площадке контакта зубьев и характеризует контактную прочность зубьев.
Обычно выкрашивание зуба происходит около полюса, где и определяется 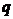 по формуле:
по формуле:
 ,
,
где 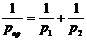
Здесь 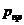 - приведенный радиус кривизны зубьев в точке контакта.
- приведенный радиус кривизны зубьев в точке контакта.
В полюсе радиусы кривизны эвольвент:
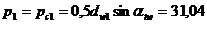
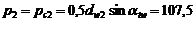
4. Синтез кулачкового механихма
Ведущее звено в кулачковом механизме называют кулачком. Ведомое – толкателем. Элементы высшей кинематической пары, принадлежащей кулачку, называют профилем кулачка, а элементы, принадлежащие толкателю, называют профилем толкателя.
Кулачковый механизм состоит из кулачка, толкателя, ролика, который закреплен на толкателе и непосредственно соприкасается с поверхностью кулачка. Ролик служит для уменьшения трения возникающего в зоне контакта кулачка с толкателем.
Полный цикл толкателя в кулачковом механизме соответствует одному полному обороту кулачка. Промежутки, соответствующие удалению из самого ближнего (по отношению к центру вращения кулачка) в самое дальнее, высотою в самом дальнем положении, возвращяются из самого дальнего положения в самое близкое, высотою в самом ближнем положении называют Ту, Твп, Тпр, Тнв.
φ Ту+φ Твп+φ Тпр+φ Тнв=360°
Задача синтеза кулачкового механизма состоит в том, чтобы построить профиль кулачковой шайбы, удовлетворяющий поставленным технологическим требованиям.
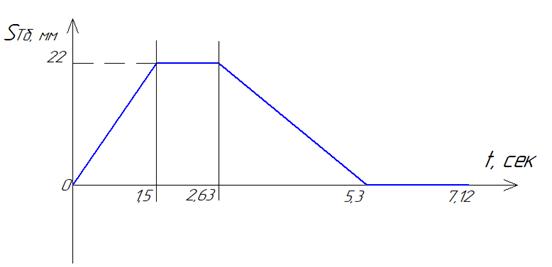
Проведем анализ зависимости S=kt+b на четырёх участках:
1 участок:

2 участок:
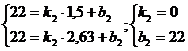
3 участок:
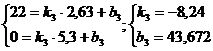
4 участок:
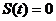 => k4 = 0, b4 = 0
=> k4 = 0, b4 = 0
Уравнения ST(t) для четырёх участков:
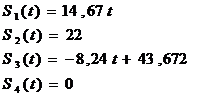
Определяем максимальную скорость толкателя Vmax = S’(t).
Получаем, что |Vmax| = 14, 67 мм/с.
Определяем требуемую угловую скорость кулачка:
ω 1 = 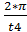 ,
,
ω = 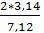 = 0, 882 рад/с
= 0, 882 рад/с
Определяем постоянную составляющую закона движения толкателя Sн:
Tgθ max = (Vmax/ω 1)/Sн
Vmax = 14, 67 мм/с
θ max- максимальный угол передачи равный 30º;
Sн = (Vmax/ω 1)/tg30°;
Sн = 28, 8 мм
Определяем радиус подшипника R:
R=0, 2*Sн,
R=0, 2*28, 8=5, 76 мм
Результаты приведены в таблице:
Таблица 4. – Расчёт профиля кулачка
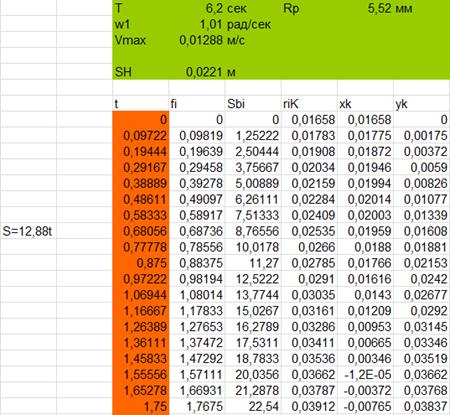

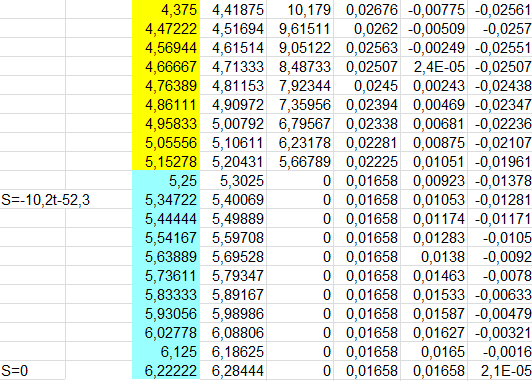

Рис. 4 – Диаграмма теоретического профиля кулачка
Литература
1. Кореняко А. С. и др. Курсовое проектирование по теории механизмов и машин. - Киев: Вища школа, 1970.
2. Попов С. А. Курсовое проектирование по теории механизмов и механике машин. - М.: Высш. шк., 1986.
3. Калабин С. Ф. Методические указания по оформлению пояснительной записки и графической части курсового проекта по курсу «Механизмы приборных и вычислительных систем». - Ижевск, 1986.
4. Артоболевский И. И. ТММ. - М: Наука, 1988.
5. Ястребов В. М. Методическое руководство к курсовому проекту по ТММ, - Ижевск, 1974 г.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|