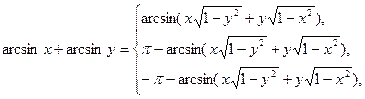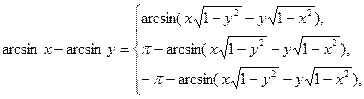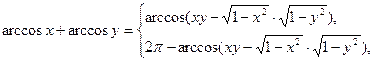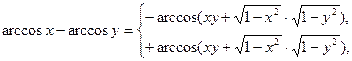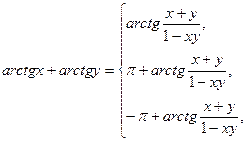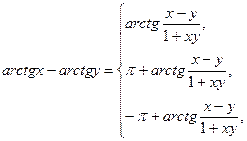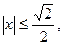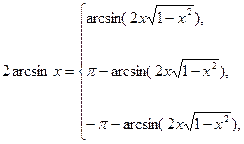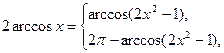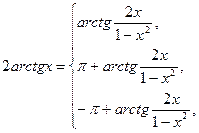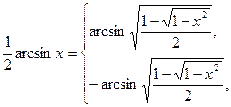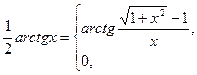- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблиця 9. Доведення.. ІІ. Формули додавання та віднімання для обернених тригонометричних . Доведення.
Таблиця 9
Формули, які виражають тригонометричні операції
над оберненими тригонометричними функціями, співвідношення між аркфункціями
І. Основні співвідношення між оберненими тригонометричними функціями
1) 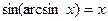 ,
, 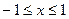 ;
;
2) 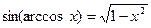 ,
, 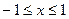 .
.
Доведення
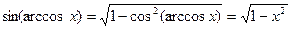 .
.
3) 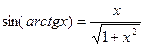 , x є R;
, x є R;
4) 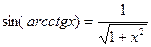 , x є R;
, x є R;
5) 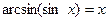 ,
, 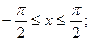
6) 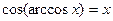 ,
, 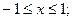
7) 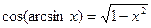 ,
, 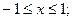
8) 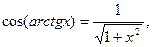 x є R;
x є R;
9) 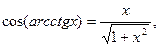 x є R;
x є R;
10) 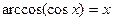 ,
, 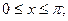
11) 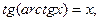 x є R;
x є R;
12) 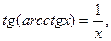
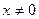 .
.
13) 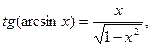 – 1< х < 1.
– 1< х < 1.
Доведення.
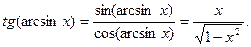
14) 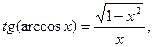
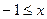 < 0, 0 <
< 0, 0 < 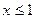 ;
;
15) 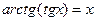 , –
, – 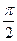 < х <
< х < 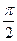 ;
;
16) 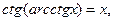 x є R;
x є R;
17) 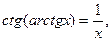
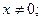
Доведення.
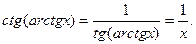
18) 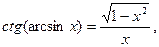
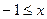 < 0, 0 <
< 0, 0 < 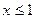 ;
;
19) 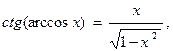 – 1< х < 1;
– 1< х < 1;
20) 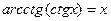 , 0 < х <
, 0 < х < 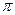 ;
;
21) 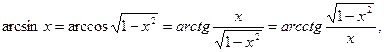 0 < x < 1;
0 < x < 1;
22) 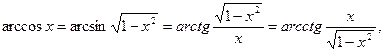 0 < x < 1;
0 < x < 1;
23) 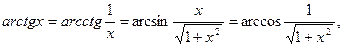 0 < x < +
0 < x < + 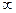 ;
;
24) 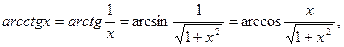 0 < x < +
0 < x < + 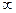 ;
;
25) 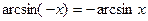 ;
;
26) 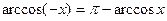 ;
;
27) 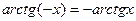 ;
;
28) 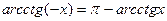 .
.
ІІ. Формули додавання та віднімання для обернених тригонометричних
функцій:
29) 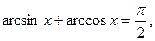
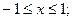
Доведення.
Так як 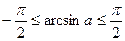 , то
, то  , а
, а 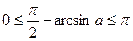 .
.
Маємо: 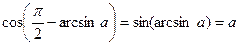 . Оскільки
. Оскільки 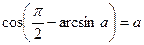 і
і 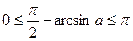 , то
, то 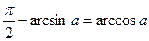 , звідки
, звідки 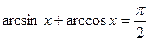 .
.
30) 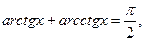 x є R;
x є R;
31) 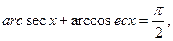
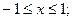
| 32) |
якщо ху ≤ 0 або х2 + у2 ≤ 1, | ||
|
якщо х > 0, у > 0 і х2 + у2 > 1, | |||
|
якщо х < 0, у < 0 і х2 + у2 > 1; | |||
|
| |||
| 33) |
якщо ху ≥ 0 або х2 + у2 ≤ 1, | ||
|
якщо х > 0, у < 0 і х2 + у2 > 1, | |||
|
якщо х < 0, у > 0 і х2 + у2 > 1;
| |||
|
| |||
| 34) | якщо х + у ≥ 0, | ||
| якщо х + у < 0; | |||
|
| |||
| 35) | якщо х ≥ у, | ||
| якщо х < у; | |||
| 36) | якщо ху < 1, |
| якщо х > 0 і ху > 1, | |
| якщо х < 0 і ху > 1; | |
| 37) | якщо ху > – 1, |
| якщо х > 0 і ху < – 1, | |
| якщо х < 0 і ху < – 1; |
ІІІ. Формули подвоєння для обернених тригонометричних функцій:
|
якщо | ||
| 38) | ||
якщо 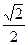 < х ≤ 1, < х ≤ 1,
| ||
якщо –1< х < – 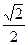 ; ;
| ||
| 39) | якщо 0 ≤ х ≤ 1, | |
| якщо –1≤ х < 0; | ||
| 40) |
якщо 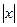 < 1, < 1,
| |
| якщо х > 1, | ||
| якщо х < – 1. |
ІV. Формули ділення обернених тригонометричних функцій на два:
| 41) | якщо 0 ≤ х ≤ 1, |
| якщо –1≤ х < 0; |
42) 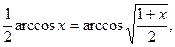
| якщо – 1 ≤ х ≤ 1; |
| 43) |
якщо 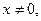
|
| якщо х = 0. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|