
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа. Вариант 0
Контрольная работа
Вариант 0
| №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 |
| В профком избрано 9 человек. Из них надо выбрать председателя, его заместителя и казначея. Сколькими способами это можно сделать? | |
| Сколькими способами можно переставить буквы слова «логарифм» так, чтобы 2-ое, 4-ое и 6-ое места были заняты согласными буквами? | |
| Наудачу выбирают 5 военнослужащих из группы, состоящей из 4 офицеров и 12 солдат. Какова вероятность того, что в группе будет не более двух офицеров? | |
| В группе 10 студентов изучают английский язык, 6 – французский и 8 – немецкий. Наугад составляется группа из трех человек. Найдите вероятность того, что все три студента изучают разные языки. | |
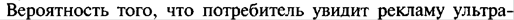

| |

| |
| Сделано два высокорисковых вклада – 20 млн. руб. в компанию А и 18 млн. руб. в компанию В. Компания А обещает 20% годовых, но может обанкротиться с вероятностью 0, 3, компания В обещает 30% годовых, но может обанкротиться с вероятностью 0, 2. Будем считать, что банкротства компаний независимы. Случайная величина Х – сумма вкладов, полученных от двух компаний через год. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график. | |

| |
| Данные среднесуточной переработки сахара (в тыс. ц) заводами сахарной промышленности некоторого региона представлены в виде ряда: 12, 0 13, 6 14, 7 18, 9 17, 3 16, 1 15, 3 18, 1 12, 9 13, 5 20, 1 16, 9 19, 1 18, 4 17, 8 15, 6 17, 4 15, 8 13, 8 14, 1 20, 8 19, 7 18, 9 19, 0 16, 1 15, 8 14, 8 16, 4 18, 4 15, 8 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о значении среднесуточной переработки сахара (в тыс. ц) заводами сахарной промышленности некоторого региона |
№1.
В профком избрано 9 человек. Из них надо выбрать председателя, его заместителя и казначея. Сколькими способами это можно сделать?
Решение
Необходимо ВЫБРАТЬ 3 человек из 9 и РАЗМЕСТИТЬ их по 3 должностям, поэтому используется формула подсчёта числа размещений:
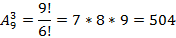
Ответ: 504 способа.
№2.
Сколькими способами можно переставить буквы слова «ЛОГАРИФМ» так, чтобы 2-ое, 4-ое и 6-ое места были заняты согласными буквами?
Решение
«ЛОГАРИФМ» состоит из 3 гласных и 5 согласных букв. Необходимо ВЫБРАТЬ и РАЗМЕСТИТЬ на 2-ое, 4-ое и 6-ое места 3 из 5 согласных букв, И РАЗМЕСТИТЬ на остальных 5 местах 5 оставшихся букв. Поэтому используются формулы подсчёта числа размещений и перестановок. Союз «и» подсказывает, что нужно использовать правило умножения: N= N1+N2,
где N1 – число способов ВЫБРАТЬ и РАЗМЕСТИТЬ на 2-ое, 4-ое и 6-ое места 3 из 5 согласных букв (размещения),
N2 – число способов РАЗМЕСТИТЬ (переставить) на остальных 5 местах 5 оставшихся букв (перестановки).
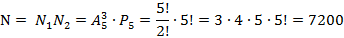
Ответ: 7200 способов.
№3.
Наудачу выбирают 5 военнослужащих из группы, состоящей из 4 офицеров и 12 солдат. Какова вероятность того, что в группе будет не более двух офицеров?
Решение
Событие A – в группе из пяти человек окажется не более двух офицеров.
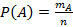 , где n – количество способов сформировать группу:
, где n – количество способов сформировать группу:
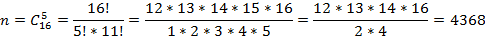
mA – количество способов сформировать группу так, чтобы в ней было не более двух офицеров, то есть ни одного ИЛИ один офицер ИЛИ два офицера.
По правилу сложения: mA=mA0+mA1+mA2, где:
mA0 – количество способов сформировать группу так, чтобы в ней не было офицеров.
mA1 – количество способов сформировать группу так, чтобы в ней был один офицер.
mA2 – количество способов сформировать группу так, чтобы в ней было два офицера.
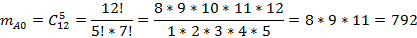
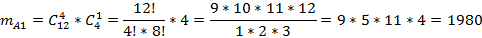
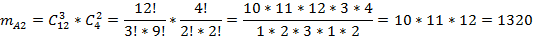
mA=792+1980+1320=4092
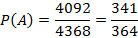
Ответ: 341/364.
№4.
В группе 10 студентов изучают английский язык, 6 – французский и 8 – немецкий. Наугад составляется группа из трех человек. Найдите вероятность того, что все три студента изучают разные языки.
Решение
Событие A – все три студента в группе изучают разные языки.
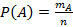 , где n – количество способов сформировать группу, то есть выбрать трех человек из 24 (сочетания);
, где n – количество способов сформировать группу, то есть выбрать трех человек из 24 (сочетания); 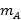 – число способов выбрать одного со знанием английского и одного со знанием французского и одного со знанием немецкого.
– число способов выбрать одного со знанием английского и одного со знанием французского и одного со знанием немецкого.
По правилу умножения mA= 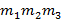 .
.
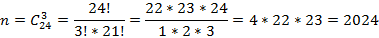
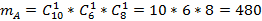
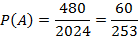
Ответ: 60/253.
№5.
Вероятность того, что потребитель увидит рекламу ультразвуковой стиральной машинки по телевидению равна 0, 7. Вероятность того, что потребитель увидит эту рекламу на рекламном стенде, равна 0, 4. Найдите вероятность того, что потребитель увидит:
А) Обе рекламы, если учесть, что события независимы;
Б) Хотя бы одну рекламу (эффективность рекламы);
В) Только одну рекламу.
Решение
События:
A1 – потребитель увидел рекламу по телевидению. P(A1)=0, 7 по условию.
A2 – потребитель увидел рекламу на стенде. P(A2)=0, 4 по условию.
B=A1A2 – Потребитель увидел обе рекламы.
C=A1+A2 – Потребитель увидел хотя бы одну рекламу.
D – Потребитель увидел только одну рекламу.
По теореме умножения, так как события A1 и A2 независимы:

По теореме сложения, так как события A1 и A2 совместны:
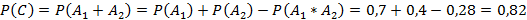
Событие D означает, что потребитель увидел рекламу ТОЛЬКО по телевидению ИЛИ ТОЛЬКО на стенде. Опираясь на теоремы сложения и умножения:
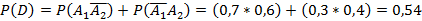
Ответ: а) 0, 28; б) 0, 82; в) 0, 54.
№6.
В вычислительной лаборатории имеется шесть клавишных автоматов и четыре полуавтомата. Вероятность того, что за время выполнения некоторого расчёта автомат не выйдет из строя, равна 0, 95, для полуавтомата вероятность равна 0, 8. Студент производит расчёт на машине, выбранной наудачу. Найдите вероятность того, что до окончания расчёта машина выйдет из строя.
Решение
Событие A – машина вышла из строя.
Гипотезы:
H1 – студент использовал автомат. P(H1)=0, 6; условная вероятность P(A/H1)=0, 05.
H2 – студент использовал полуавтомат. P(H2)=0, 4; условная вероятность P(A/H2)=0, 1.
По формуле полной вероятности:
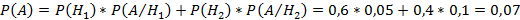
Ответ: 0, 07.
№7.
Сделано два высокорисковых вклада – 20 млн. руб. в компанию А и 18 млн. руб. в компанию В. Компания А обещает 20% годовых, но может обанкротиться с вероятностью 0, 3, компания В обещает 30% годовых, но может обанкротиться с вероятностью 0, 2. Будем считать, что банкротства компаний независимы. Случайная величина Х – сумма вкладов, полученных от двух компаний через год.
Найти:
а) закон распределения этой случайной величины;
б) построить многоугольник распределения;
в) вычислить математическое ожидание;
г) определить дисперсию;
д) составить функцию распределения F(x) и построить ее график
| Компания | Размер вклада (млн. руб. ) | % годовых | Вероятность банкротства |
| A | 0, 3 | ||
| B | 0, 2 |
X является дискретной случайной величиной. Её закон распределения:
| xi | 23, 4 | 47, 4 | ||
| pi | 0, 06 | 0, 24 | 0, 14 | 0, 56 |
Для случая банкротства обеих компаний:
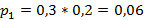
Для случая банкротства только компании A:
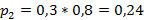
Для случая банкротства только компании B:
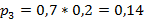
Для случая выживания обеих компаний:
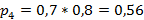
Многоугольник распределения:
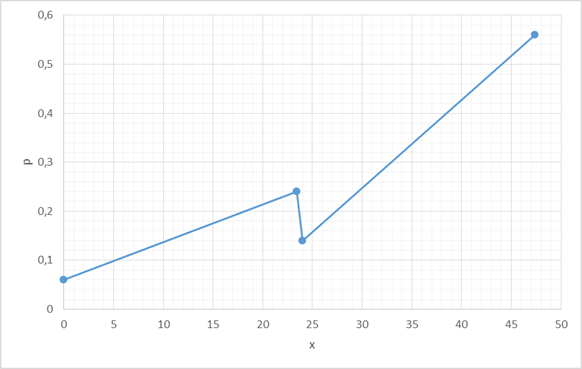
Математическое ожидание и дисперсия:
| xi | pi | xipi | xi2 | xi2pi |
| 0, 06 | ||||
| 23, 4 | 0, 24 | 5, 616 | 547, 56 | 131, 4144 |
| 0, 14 | 3, 36 | 80, 64 | ||
| 47, 4 | 0, 56 | 26, 544 | 2246, 76 | 1258, 186 |
| M[X]= | 35, 52 | M[X2]= | 1470, 24 |
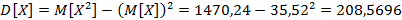
Функция распределения:
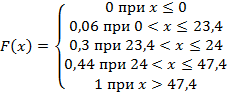
График функции распределения:
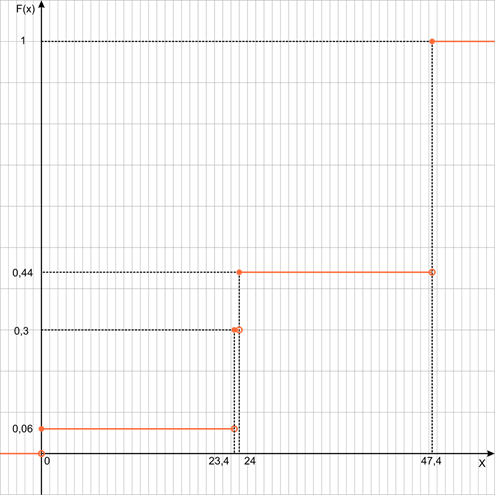
Ответ: M[X]=35, 52; D[X]=208, 5696.
№8.
Применяемый метод лечения приводит к выздоровлению в 90% случаев. Какова вероятность того, что из пяти больных поправится не менее четырёх человек?
Решение
Из условия:
P = 0, 9 => q = 1-0, 9 = 0, 1
n = 5
4 ≤ k ≤ 5 => k = 4 или k = 5
Требуется найти 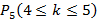
Параметр k может принимать два значения, n мало, следовательно, используем формулу Бернулли для вычисления каждого слагаемого:
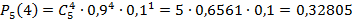
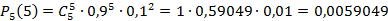
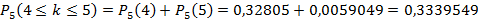
Ответ: 0, 3339549.
№9.
Данные среднесуточной переработки сахара (в тыс. ц) заводами сахарной промышленности некоторого региона представлены в виде ряда:
12, 0 13, 6 14, 7 18, 9 17, 3 16, 1 15, 3 18, 1 12, 9 13, 5
20, 1 16, 9 19, 1 18, 4 17, 8 15, 6 17, 4 15, 8 13, 8 14, 1
20, 8 19, 7 18, 9 19, 0 16, 1 15, 8 14, 8 16, 4 18, 4 15, 8
а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор).
б) Изобразить его графически (в виде полигона частостей или гистограммы).
в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности.
г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение.
д) Сделать вывод о значении среднесуточной переработки сахара (в тыс. ц) заводами сахарной промышленности некоторого региона
Решение
Имеем непрерывную случайную величину с малым количеством повторов значений, следовательно, строим интервальный вариационный ряд.
Найдём наибольший и наименьший элементы выборки:
Xнаиб=20, 8
Xнаим=12, 0
Определим размах ряда:

Определим длину интервала по формуле:

Выбрали значение длины интервала с четной цифрой в конце, чтобы упростить дальнейшие вычисления.
Определим Xнач 1го интервала:
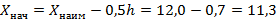
Найдём границы интервалов и вычислим соответствующие частоты для каждого интервала(11, 3+1, 4=12, 7; 12, 7+1, 4=14, 1 и т. д)
| 11, 3 | 12, 7 | 14, 1 | 15, 5 | 16, 9 | 18, 3 | 19, 7 | 21, 1 | ||||||||
Составим таблицу:
| Интервал xi - xi+1 | Середина интервала ni | Частота интервала mi | Относит. частота

| Плотность относит. частот
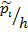
| Накопленные частости
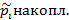
|
| 11, 3-12, 7 | 0, 03 | 0, 024 | 0, 03 | ||
| 12, 7-14, 1 | 13, 4 | 0, 1 | 0, 071 | 0, 13 | |
| 14, 1-15, 5 | 14, 8 | 0, 17 | 0, 119 | 0, 3 | |
| 15, 5-16, 9 | 16, 2 | 0, 23 | 0, 167 | 0, 53 | |
| 16, 9-18, 3 | 17, 6 | 0, 17 | 0, 119 | 0, 7 | |
| 18, 3-19, 7 | 0, 2 | 0, 143 | 0, 9 | ||
| 19, 7-21, 1 | 20, 4 | 0, 1 | 0, 071 |
В предпоследнем столбце таблицы получим значения выборочной функции плотности распределения 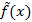 . Построим гистограмму функции:
. Построим гистограмму функции:
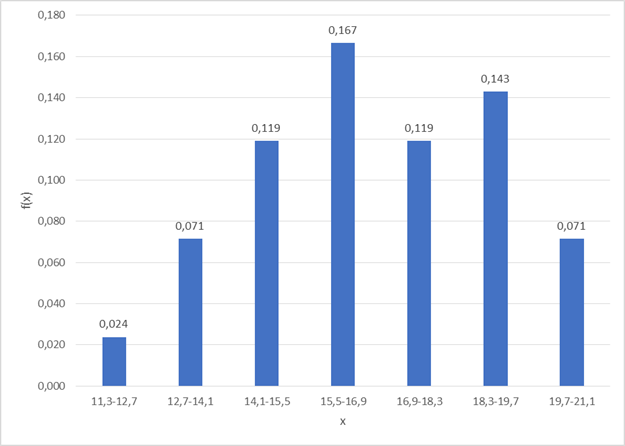
В последнем столбце получим значения выборочной функции распределения 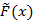 . Построим график функции:
. Построим график функции:

Вычислим выборочную среднюю 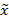 , используя значения ni и mi:
, используя значения ni и mi:
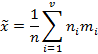
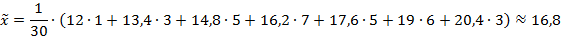
Определим выборочную дисперсию 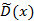 и среднее квадратическое отклонение:
и среднее квадратическое отклонение:
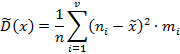
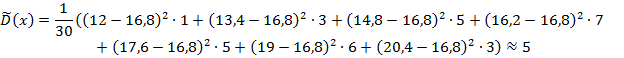
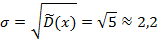
Вывод: Значение среднесуточной переработки сахара заводами сахарной промышленности некоторого региона в среднем равно 16, 8 ±2, 2 тыс. ц.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|