
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
1. Метод интегрирования по частям
Отчеты по дистанционным заданиям вы делаете в двух видах:
1 - фото после каждого занятия Чигринец А. В,
2 – конспекты с которыми Вы придете в техникум. Это будет доказательство Вашей работы и допуск к экзамену.
Выполняем и высылаем на электронный адрес chigrinecc@yandex. ru или на вайбер по моему номеру 0713691309.
24. 03. 2022
Математика
Группа 11КС
План
1. Метод интегрирования по частям
2. Решение примеров.
МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Формула интегрирования по частям имеет вид
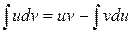 ,
,
где 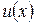 и
и 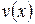 – дифференцируемые функции.
– дифференцируемые функции.
Для интегралов вида 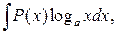
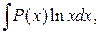
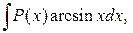
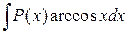 ,
, 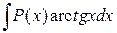 ,
, 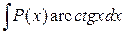 за
за 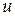 принимаются соответственно функции
принимаются соответственно функции 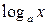 ,
, 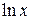 ,
, 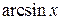 ,
, 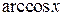 ,
, 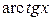 ,
, 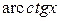 .
.
Для интегралов вида 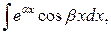
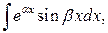
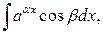
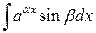 за
за 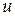 можно принять любую из функций, но здесь требуется двукратное интегрирование по частям.
можно принять любую из функций, но здесь требуется двукратное интегрирование по частям.
Пример. Вычислить интеграл 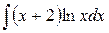 .
.
Решение. Полагая 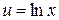 ,
, 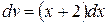 , имеем
, имеем 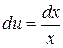 ,
, 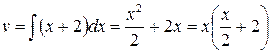 , следовательно,
, следовательно,

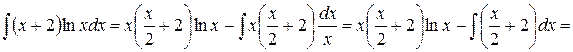
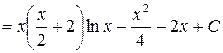 .
.
Пример. Вычислить интеграл 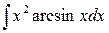 .
.
Решение. Полагая 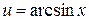 ,
, 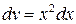 , имеем
, имеем 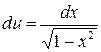 ,
, 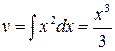 , следовательно,
, следовательно,
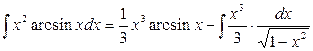 . .
| (а) |
Теперь найдем интеграл в правой части равенства (а) с помощью подстановки 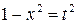 . Дифференцируя, получаем
. Дифференцируя, получаем 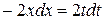 или
или 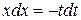 , следовательно,
, следовательно,
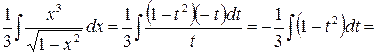
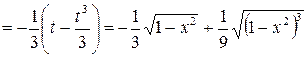 .
.
Подставляя этот результат в равенство (а), находим
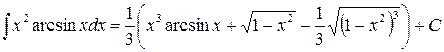 .
.
Пример. Вычислить интеграл 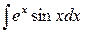 .
.
Решение. Для интегрирования по частям, полагая 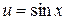 ,
, 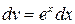 , имеем
, имеем 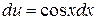 ,
, 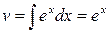 , следовательно,
, следовательно,
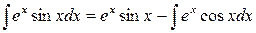 . .
| (в) |
Интеграл в правой части снова интегрируем по частям. Полагая 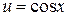 ,
, 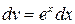 , имеем
, имеем 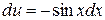 ,
, 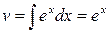 , следовательно,
, следовательно,
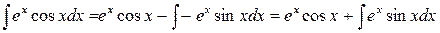 .
.
Подставляя этот результат в равенство (в), получаем
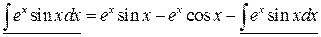 ,
,
приведем подобные элементы
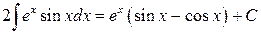 .
.
Следовательно,
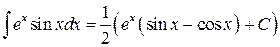 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|